Задачи, приводящие к дифференциальным уравнениям.

Общие сведения о дифференциальных уравнениях.

Материальная точка массы m замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости V. Найти зависимость скорости от времени. Найти скорость точки через 3 с после начала замедления, если V(0) = 100 м/с, a V(l)= 50 м/с.

Решение: Примем за независимую переменную время t,отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки V будет функцией t, т. е. V = V(t). Для нахождения V(t)воспользуемся вторым законом Ньютона (основным законом механики):
та=F, где а=V'(t) — есть ускорение движущегося тела, F — результирующая сила, действующая на тело в процессе движения.

В данном случае F =— kV², k > 0 —- коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция V = V(t) является решением дифференциального уравнения тV' =— k V² или V' = —kV²/m. Здесь т — масса тела.

Из того, что 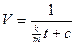, где с – const. Найдя зависимость скорости от времени, легко найти скорость точки через 3 с после начала замедления.

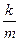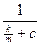Найдем сначала параметры и с. Согласно условию задачи, имеем: V(0)= =100 и V(l)= = 50. Отсюда с = 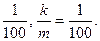Следовательно, скорость точки изменяется по закону V = 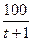. Поэтому V(3) = 25 м/с.