ПРОГНОЗУВАННЯ В РАЗІ МНОЖИННОЇ РЕГРЕСІЇ
У розд.5 ми показали, як оцінена модель двовимірної регресії може бути застосована для середнього прогнозу, тобто прогнозування для функції популяції регресії (PRF), а також для індивідуального прогнозу, тобто прогнозування індивідуального значення величини Y для фіксованого значення регресора X0.
Оцінене рівняння множинної регресії також може бути використане для прогнозу. Його методика є простим поширенням двовимірного випадку й ґрунтується на тих же формулах за винятком формул для оцінок дисперсії і стандартних похибок прогнозованих величин.
Проілюструємо це на прикладі середнього й індивідуального прогнозів для моделі особистих витрат на споживання в США в 1956–1970 рр.:
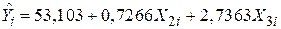 (13,0261) (0,0487) (0,8486)
R2=0,9988,
(13,0261) (0,0487) (0,8486)
R2=0,9988,
| (8.1) |
де Y – особисті витрати на споживання; X2 – особистий дохід; X3 – змінна тренда.
Як нам відомо 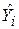 є оцінка величини
є оцінка величини 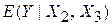 істинного середнього значення Y для заданих значень X2 і X3.
істинного середнього значення Y для заданих значень X2 і X3.
Припустимо, що для 1971 р. маємо X2=567 і X3=16. Підставляючи ці значення в (8.1), одержуємо
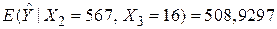 . .
| (8.2) |
Отже, середні особисті витрати на споживання для 1971 р. складають приблизно 509 млрд дол. Із причин, указаних раніше, 509 млрд дол. також є індивідуальним прогнозом для 1971 р., тобто Y1971. Проте дисперсії для середнього 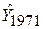 й індивідуального Y1971 прогнозів різні. Для їх обчислення найзручніше використовувати матричний апарат. Можна показати, що
й індивідуального Y1971 прогнозів різні. Для їх обчислення найзручніше використовувати матричний апарат. Можна показати, що
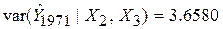 і і 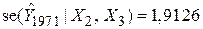 ; ;
| (8.3) |
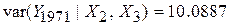 і і 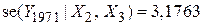 . .
| (8.4) |
При виконанні припущень класичної моделі регресії ми тепер можемо побудувати 10(1–a)-довірчий інтервал для середнього прогнозу:
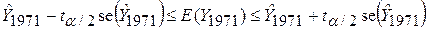 . .
|
Зрозуміло, що подібну процедуру можна виконати й для будь-яких інших значень Х2 і Х3.
100(1–a)-довірчий інтервал для індивідуального прогнозу Y1971 складає
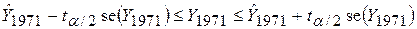 . .
|
Для нашого прикладу ми одержуємо довірчий інтервал для середнього прогнозу
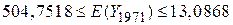 . .
|
Довірчий інтервал для індивідуального прогнозу має вигляд
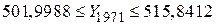 . .
|
Кількість степенів вільності для ta/2 є (n–3) для моделі з трьома змінними і (n–k) для моделі з k змінними.
Дата добавления: 2016-07-27; просмотров: 1817;











