Перевірка структурної стабільності моделей регресії
У табл. 7.7 наведені дані про особисті заощадження й особистий дохід у Великобританії в період 1946–1963 рр.
Таблиця 7.7
| Рік | Заощадження, млрд дол. | Дохід, млрд дол. |
| 0,36 | 8,8 | |
| 0,21 | 9,4 | |
| 0,08 | 10,0 | |
| 0,20 | 10,6 | |
| 0,10 | 11,0 | |
| 0,12 | 11,9 | |
| 0,41 | 12,7 | |
| 0,50 | 13,5 | |
| 0,43 | 14,3 | |
| 0,59 | 15,5 | |
| 0,90 | 16,7 | |
| 0,95 | 17,7 | |
| 0,82 | 18,6 | |
| 1,04 | 19,7 | |
| 1,53 | 21,1 | |
| 1,94 | 22,8 | |
| 1,75 | 23,9 | |
| 1,99 | 25,2 |
Припустимо, ми хочемо визначити, як особисті заощадження пов’язані з особистим доходом, тобто ми хотіли б отримати оцінку функції заощаджень. Якщо звернутися до даних з табл. 7.7, то можна відзначити, що характер заощаджень по відношенню до доходу в період 1946–1954 рр., післявоєнний (реконструктивний) період, відрізняється від періоду 1955–1963 рр., який називатимемо постреконструктивним. Інакше кажучи, функція заощаджень зазнає структурних змін між цими двома періодами, у тому розумінні, що її параметри змінюються.
Для перевірки цього факту припустимо, що функція заощаджень для двох періодів має такий вигляд:
- реконструктивний період:
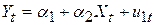 , t=1, 2,…n1; , t=1, 2,…n1;
| (7.5.1) |
- постреконструктивний:
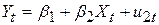 , t=1, 2,…n2, , t=1, 2,…n2,
| (7.5.2) |
де Y – особисті заощадження; X – особистий дохід; 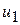 і
і 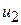 – збурюючі складові, а n1, n2 – кількість спостережень у перший і другий періоди відповідно. Кількість спостережень в періодах може збігатися або ні.
– збурюючі складові, а n1, n2 – кількість спостережень у перший і другий періоди відповідно. Кількість спостережень в періодах може збігатися або ні.
Структурні зміни функції заощаджень означають, що параметри регресій можуть відрізнятися. Зрозуміло, якщо не спостерігаються структурні зміни, то всі дані можна об’єднати й оцінити на їх підставі одну функцію заощаджень
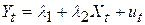 . .
| (7.5.3) |
Для з’ясування, чи існують насправді структурні зміни функції заощаджень застосовують тест Чоу.
Цей тест ґрунтується на таких двох припущеннях:
- 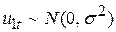 ,
, 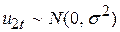 , тобто обидва стохастичні складоваи розподілені нормально і мають однакові дисперсії;
, тобто обидва стохастичні складоваи розподілені нормально і мають однакові дисперсії;
- 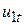 і
і 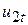 розподілені незалежно.
розподілені незалежно.
Тест Чоу складається з чотирьох етапів:
1. Об’єднуємо спостереження n1 і n2, знаходимо оцінку (7.5.3) і підраховуємо суму квадратів залишків RSS, назвемо її s1 з (n1+n2–k) степенями вільності. Тут k – кількість оцінених параметрів у рівнянні регресії (у нашому випадку2);
2. Виконуємо регресії (7.5.1) і (8.82) і одержуємо їх RSS, скажімо, s2 і s3 з (n1–k) і (n2–k) кількістю степенів вільності, відповідно. Складаємо ці RSS і знаходимо s4=s2+s3 з (n1+n2–2k) степенями вільності;
3. Одержуємо s5=s1+s4.
Дата добавления: 2016-07-27; просмотров: 1455;











