Припущення класичної лінійної моделі регресії

Скалярне позначення	Матричне позначення
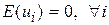
1.	E(U)=0, де Uі 0є n´1 вектори-стовпці, 0– нульовий вектор
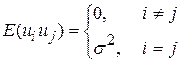
2.	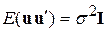, де I– n´n одинична матриця
3. Х2, Х3,…, Хk нестохастичні й фіксовані	n´k матриця Xє нестохастичною, тобто вона складається із сукупності фіксованих чисел
4. Не існує точного лінійного зв’язку між змінними X, тобто немає мультиколінеарності	Ранг матриці X дорівнює k, де k – кількість стовпців в X, при чому k<n
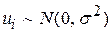
5. При перевірці гіпотез	Вектор u має багатовимірний нормальний розподіл, тобто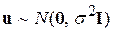

Припущення 1 (табл. 9.1) означає, що математичне сподівання збурюючого вектора u, тобто кожної його компоненти, дорівнює нулю. Більш точно 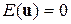означає

.

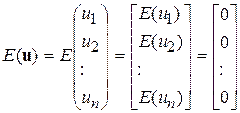(9.2.1)

Припущення 2 являє собою компактний вираз двох припущень, зображених у скалярному вигляді рівняннями (3.2.5) і (3.2.2). Щоб переконатися в цьому, можна записати

,

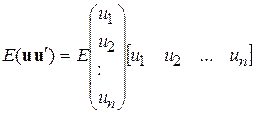де 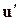– транспонований вектор-стовпець u, тобто вектор-рядок.

Виконавши перемножування матриць, отримаємо

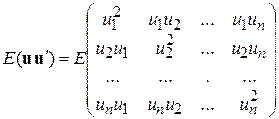
або

.

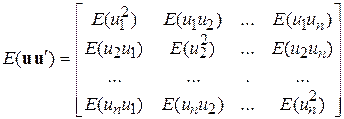(9.2.2)

Враховуючи гіпотезу про гомоскедастичність і відсутність серійної кореляції, можна подати(9.2.2) у вигляді

,

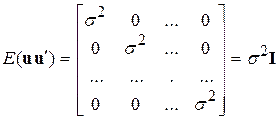(9.2.3)

де I– n´n одинична матриця.

Матриця (9.2.2) називається матрицею варіації збурень 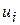; елементи головної діагоналі цієї матриці позначають дисперсії, а решта елементів – коваріації. Зазначимо, що ця матриця симетрична.

Припущення 3 стверджує, що матриця Xнестохастична, тобто її елементи – фіксовані числа.

Припущення 4 стверджує, що ранг матриці дорівнює k, тобто дорівнює кількості стовпців матриці. Це означає, що стовпці матриці лінійно незалежні, тобто не існує точного лінійного зв’язку між змінними Х. Іншимисловами, відсутня мультиколінеарність. У скалярних позначеннях це означає, що не існує множини чисел 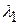, ,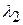… , 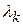з яких не всі дорівнюють нулю, тобто

,

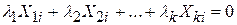(9.2.4)

де 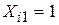для всіх i. У матричних позначеннях (9.2.4) може бути подане у вигляді

,

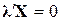(9.2.5)

де 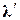– 1´k-вектор-рядок, а X– k´1-вектор-стовпець.

Якщо лінійне співвідношення вигляду (9.2.4) існує, то говорять, що змінні колінеарні. Якщо ж ця рівність можлива тільки при 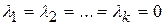, то говорять, що змінні Х лінійно незалежні.

Оцінювання за МНК

Щоб отримати оцінку вектора b запишемо функцію SRF (вибіркову функцію регресії) з k змінними в матричному вигляді:

.

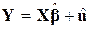(9.3.1)

Так само, як і у разі дво- й тривимірних моделей, МНК для k-вимірноїмоделі полягає в мінімізації

.

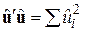(9.3.2)

Із (9.3.1) ми одержуємо

.

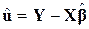(9.3.3)

Отже,

.

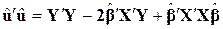(9.3.4)

Тут ми скористалися властивостями транспонування матриць, а саме 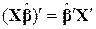. Крім того, оскільки 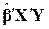є скаляр, то він не змінюється при транспонуванні .

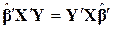У скалярних позначеннях МНК полягає в оцінюванні 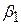, ,… 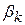таким чином, щоб 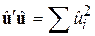була якомога малою величиною. Це досягається шляхом диференціювання (9.3.4) за 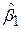, ,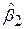… 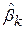і прирівнювання частинних похідних до нуля. Ця процедура приводить до системи k лінійних алгебраїчних рівнянь з k невідомими. Можна показати, що ця система має вигляд

.

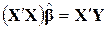(9.3.5)

Відзначимо деякі властивості матриці :

1) вона дає ряд суми квадратів і попарних добутків змінних Х. Елементи головної діагоналі являють собою ряд сум квадратів, а елементи зовні головної діагоналі – суму попарних добутків;

2) матриця симетрична, оскільки сума добутків 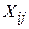і ;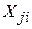

3) матриця має порядок k´k.

У (9.3.5) відомими величинами є і 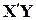, а невідомою – 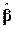. Розв’язуючи рівняння (9.3.5), знаходимо

.

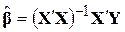(9.3.6)

Рівняння (9.3.6) відображає фундаментальний результат теорії МНК у матричній формі. Воно показує, що оцінка вектора 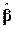може бути проведена за наявними даними.