МНОЖИННА РЕГРЕСІЯ. МАТРИЧНИЙ МЕТОД

9.1. Лінійна модель регресії з k змінними

Поширимо дво- і тривимірні моделі лінійної регресії на випадок моделі з k змінними у функції PRF, що містить залежну змінну Y і (k–1) пояснювальну змінну. Відповідну функцію PRF можна подати у вигляді

,

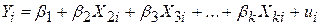(9.1.1)

де 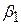– коефіцієнт, що визначає значення Y при нульових значеннях вхідних змінних; , ,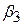… 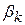– частинні кутові коефіцієнти, u – стохастичний збурюючий складова, i – спостереження, n – розмір вибірки. Рівняння (9.1.1) можна інтерпретувати звичайним способом, а саме: воно дає середнє або очікуване значення величини Y при фіксованих значеннях X₂, X₃,…X_k, тобто .

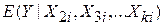Це рівняння є скороченим записом таких рівнянь:

, , ................ .

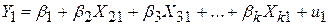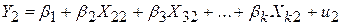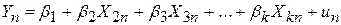(9.1.2)

Подамо цю систему рівнянь у матричному вигляді

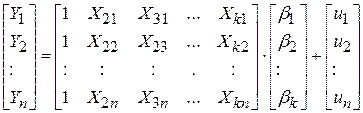
(9.1.3)

або

,

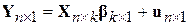(9.1.4)

де Y– вектор-стовпець спостережень залежної змінної Y, розміром n´1; Х– матриця спостережень розміром n´k, перший стовпець якої складається з одиниць, а наступні – дані змінних від X₂до X_k; b – вектор-стовпець незалежних параметрів 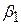, ,… 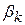розміром k´1; u– вектор-стовпець n збурень u_i розміром n´1.

У випадках, коли не виникає плутанини щодо розмірів або порядків матриці Xі векторів Y, bйuрівняння (9.1.4) може бути записане в простому вигляді

.

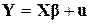(9.1.5)

Для ілюстрації матричного методу розглянемо модель «доходи-витрати на споживання» з двома змінними, вивчену нами раніше (розд. 3):

,

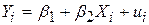де 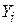– витрати на споживання, а 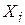– дохід. Використовуючи дані табл. 3.2, отримаємо

.

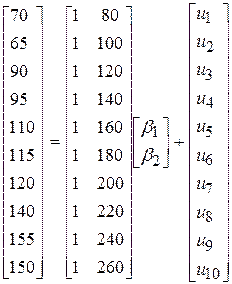(9.1.6)

Так само, як і у випадках моделей з двома або трьома змінними, нашою метою є проведення оцінювання регресії (9.1.1), складання висновків на підставі наявних даних. Для оцінювання ми можемо, як і раніше, використовувати МНК.