Частинні коефіцієнти кореляції

Раніше ми розглядали коефіцієнт кореляції R, що дає міру степеня лінійної асоційованості між двома змінними. Для моделі регресії з трьома змінними можемо підрахувати вже три коефіцієнти кореляції: R₁₂ (кореляція між Y і X₂), R₁₃ (між Y і X₃) і R²₃ (між X₂ і X₃). Відзначимо, що індекс 1 ми відносимо до Y, а 2 і 3 до X₂ і X₃ відповідно. Ці кореляційні коефіцієнти називаються простими кореляційними коефіцієнтами, або коефіцієнтами нульового порядку. Їх можна підрахувати за відомою формулою

.

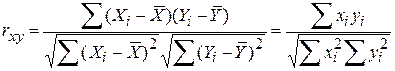Розглянемо тепер, чи дійсно, скажімо, R₁₂ дає “істинний” степінь лінійної асоційованості між Y і X₂, коли третя змінна X₃ асоційована з ними. Припустимо, що істинна модель регресії задається рівністю

.

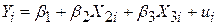Ми не включатимемо в модель змінну X_3i і побудуємо регресію Y тільки за X₂ з кутовим коефіцієнтом b₁₂. Чи буде цей коефіцієнт дорівнювати “істинному” коефіцієнту . У загальному випадку R₁₂ не відображає істинний степінь асоційованості між Y і X₂ у присутності X₃. Як ми пізніше покажемо, він дає спотворене уявлення про природу асоціативності між Y і X₂. Отже, нам потрібен такий коефіцієнт кореляції, який не залежав би від впливу X₃ ні на X₂, ні на Y. Такий кореляційний коефіцієнт можна отримати, і він називається частинним коефіцієнтом кореляції. Концептуально він аналогічний частинному коефіцієнту регресії. Частинні коефіцієнти кореляції вводяться таким чином:

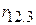- – частинний коефіцієнт кореляції між Y і X₂ при постійному значенні X₃;

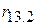- – частинний коефіцієнт кореляції між Y і X₃ при постійному значенні X₂;

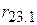- – частинний коефіцієнт кореляції між X₂ і X₃ при постійному значенні Y.

Один із шляхів визначення частинних коефіцієнтів кореляції полягає в такому. Регресуємо Y за X₃ таким чином:

.

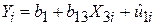Проводимо регресію Х₂ за Х₃:

.

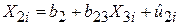Звернемо увагу на те, що залишки 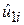є величиною 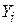після «звільнення» її від впливу змінної Х₃. Аналогічно 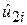– величина 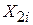після «звільнення» її від впливу змінної Х₃. Тепер ми можемо регресувати 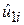за 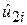і тим самим знайти простий коефіцієнт кореляції 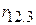, оскільки значення Х₃ залишається постійним. Одержуємо

.

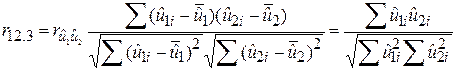(5.8.1)

При цьому ми врахували, що .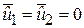

Із вищезазначеного зрозуміло, що частинний коефіцієнт кореляції між Y і Х₂ при постійному Х3 є простий (нульового порядку) коефіцієнт кореляції між залишками від регресії Y за Х₃ і Х₂ за Х₃ відповідно. Аналогічним чином інтерпретуються коефіцієнти кореляці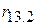ї і .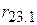

На практиці, проте, немає необхідності проводити цю процедуру, що складається з трьох етапів. Для обчислення частинних коефіцієнтів кореляції можна застосувати формули, що виражають їх через прості коефіцієнти кореляції:

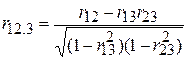;	(5.8.2)
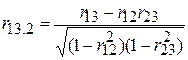;	(5.8.3)
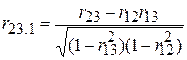.	(5.8.4)

Визначені таким чином величини називаються коефіцієнтами кореляції першого порядку. Під порядком ми маємо на увазі кількість індексів, що стоять після крапки. Так 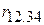– другого порядку, а 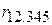– третього. Як наголошувалося раніше, 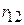і – прості або нульового порядку. Інтерпретація, скажімо, 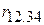така, що існує коефіцієнт кореляції між Y і X₂ при постійних значеннях X₃ і X₄.