Проста регресія в контексті множинної регресії

Припущення (5.1.6) класичної лінійної регресії стверджує, що модель регресії коректно специфікована, тобто помилка зсуву внаслідок неправильної специфікації відсутня. Наведені в попередніх розділах відомості дозволяють пояснити це твердження.

Припустимо, що (5.5.7) є “істинна” модель, що пояснює рівень дійсної інфляції за допомогою рівня безробіття й рівня очікуваної інфляції. Водночас припустимо, що хтось застосовує таку модель регресії:

,

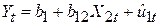(5.6.1)

де Y_t – дійсний на момент часу t рівень інфляції; Х_2t – рівень безробіття на той же момент часу; 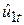– залишковий складова. Кутовий коефіцієнт b₁₂ визначає зміну середнього рівня інфляції, викликану одиничною зміною рівня безробіття.

Оскільки «істинною моделлю» є (5.6.1), та рівність (5.6.1) має помилку специфікації, яка полягає у відсутності в моделі змінної Х₃ очікуваного рівня інфляції.

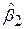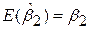Ми знаємо, що у множинній регресії (5.5.7) є незміщеною оцінкою , тобто . Чи може коефіцієнт b₁₂ простої регресії Y по Х₂ також бути незміщеною оцінкою ? Тобто чи виконуватиметься 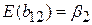? У термінах нашого прикладу це питання можна сформулювати таким чином. Чи буде коефіцієнт рівня безробіття в (5.6.1) давати незміщену оцінку істинного впливу на рівень інфляції, якщо ми знаємо, що в рівняння не включена змінна Х₃ (очікуваний рівень інфляції)? У загальному випадку відповідь звучить так: b₁₂ не буде незміщеною оцінкою . Крім того, var(b₁₂) може бути зміщеною оцінкою 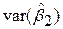. Можна показати, що насправді виконується рівність

,

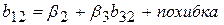(5.6.2)

де b₃₂ – кутовий коефіцієнт у регресії Х₃ за Х₂, тобто

.

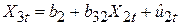(5.6.3)

Із (5.6.2) можна отримати рівність

.

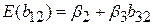(5.6.4)

За даними вибірки b₂₃ обчислюється за формулою

.

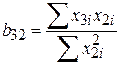Як бачимо з рівняння (5.6.3), у випадку 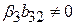коефіцієнт b₁₂ є зміщеною оцінкою 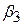. Якщо 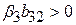, то зсув буде у бік завищення, а у випадку 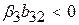– у бік заниження.

Із цього випливає, що згідно з (5.6.2), коефіцієнт простої регресії b₁₂ враховує не тільки «прямий», або «нетто», вплив Х₂ на Y (при фіксованому значенні впливу Х₃), але й непрямий вплив на Y через невключену змінну Х₃. Коротше кажучи, b₁₃ визначає «загальний ефект» (прямий + непрямий) Х₂ на Y, тоді як 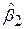позначає тільки прямий ефект впливу Х₂ на Y, оскільки вплив Х₃ зберігається фіксованим.

Зі сказаного вище робимо висновок: загальний ефект Х₂ на Y (=b₁₂) складається з прямого (=b₂) та непрямого (=b₃b₃₂) ефекту Х₂ на Y.

У визначеннях нашого прикладу це звучить таким чином. Загальний вплив одиничної зміни рівня безробіття на дійсний рівень інфляції складається з прямого впливу (при фіксованому рівні очікуваної інфляції) і непрямого ефекту через дію безробіття на очікуваний рівень інфляції. Цей результат може бути пояснений за допомогою діаграми (рис.5.2).

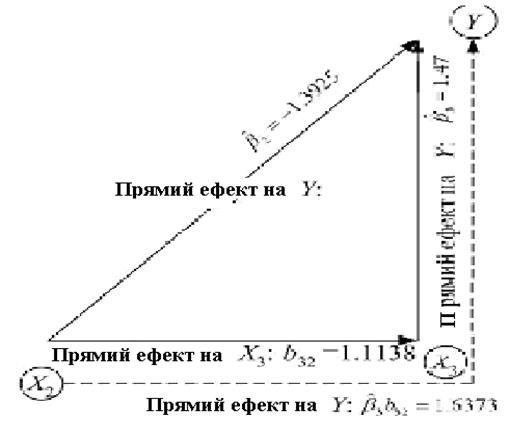
Рис. 5.2. Прямий і непрямий ефекти Х₂ на Y

Проілюструємо теоретичне міркування на прикладі кривої Філіпса.

Використовуючи дані табл.5.1, одержуємо для моделі (5.6.1) такі результати:

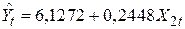(4,2853) (0,6304) t = (1,4298) (0,3885) R2=0,135.

(5.6.5)

Несподіваним в (5.6.5) є те, що b₁₂=0.2448 не тільки має позитивний знак (позитивний кутовий коефіцієнт кривої Філіпса), але також мало відрізняється від нуля. Водночас у (5.6.2) ми бачимо, що 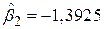не тільки має очікуваний негативний знак, але й статистично значно відрізняється від нуля, що пояснюється непрямим ефектом доданку b₃b₃₂ з (5.6.4). Із (5.5.8) ми знаємо, що 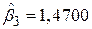. Для знаходження b₃₂ виконаємо регресію (5.6.2) за наявними даними:

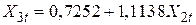(2,7267) (0,4011) t = (–0,2659) (2,7769), r=0,4120.

(5.6.6)

Значення b₃₂=1,1138 позначає, що збільшення Х₂ на одиницю приводить до зростання (в середньому) Х₃ приблизно на 1,11 одиниць. Але якщо на цю величину зросте Х₃, то її дія на Y буде 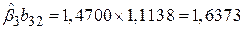. Отже, з (5.6.2) ми маємо остаточно

.

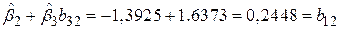Із наведених міркувань можна зробити такий висновок. Якщо з якоїсь причини ухвалити рішення про застосування моделі тривимірної регресії, не слід звертатися до найпростішої двовимірної регресії. У більш загальному випадку це звучить так. Якщо ви віддали перевагу конкретній моделі регресії і вважаєте її «істинною», то не слід модифікувати її шляхом виключення з моделі якої-небудь змінної. Якщо ви знехтуєте цією рекомендацією, то отримаєте зміщені оцінки параметрів. Крім того, ви можете отримати хибне значення 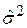і некоректні довірчі інтервали для параметрів регресії. Звернемо увагу, що стандартна похибка коефіцієнта 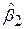в моделі (5.5.8) набагато менша (у порівнянні з величиною 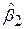), ніж у моделі (5.6.5). Тому довірчі інтервали й перевірка гіпотез на підставі (5.5.8) мають більший ступінь довіри, ніж за моделлю (5.6.5).

5.7. R²і скорегований R²

Коефіцієнт детермінації R² є неспадна функція від кількості пояснювальних змінних або регресорів у моделі. При збільшенні кількості регресорів R² майже неминуче зростає і ніколи не спадає. Інакше кажучи, додавання змінної Х до моделі не зменшить R². Щоб переконатися в цьому, пригадаємо визначення коефіцієнта детермінації:

.

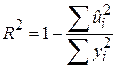(5.7.1)

Величина 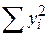не залежить від кількості змінних Х у моделі, оскільки це просто 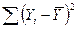. Величина RSS 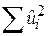, проте, залежить від кількості присутніх у моделі регресорів. Зрозуміло, що при зростанні кількості змінних Х величина 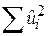повинна спадати (принаймні не зростати). Отже, R² зростатиме. Враховуючи це, при порівнянні двох моделей регресії з однаковою залежною змінною, але різною кількістю змінних Х, потрібно бути дуже обережними з наданням переваги моделі з більш високим R².

Порівнюючи два коефіцієнти детермінації R², потрібно обов’язково враховувати кількість регресорів Х, присутніх у моделі. Це можна зробити, якщо скористатися визначенням альтернативного коефіцієнта детермінації, обчислюваного за такою формулою:

,

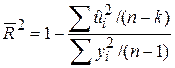(5.7.2)

де k – кількість параметрів у моделі (для моделі з трьома змінними k=3). Визначений таким чином коефіцієнт детермінації називається скоректованим R² і позначається . Термін «скорегований» позначає скоректованість за кількістю степенів вільності, пов’язаних із сумами квадратів, що входять в (5.7.2). 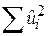має (N–k) степенів вільності. У разі моделі з трьома змінними ми знаємо, що 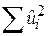має (N–3) степенів вільності.

Рівняння (5.7.2) можна також переписати у вигляді

,

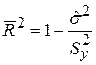(5.7.3)

де 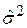– дисперсія залишків, а 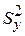– вибіркова дисперсія Y: .

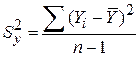Легко показати, що R² і пов’язані між собою співвідношенням

.

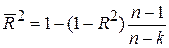(5.7.4)

Цю рівність можна отримати, якщо підставити (5.7.1) у (5.7.2). Із (5.7.4) бачимо, що для k>1 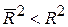, а це означає, що при збільшенні змінних Х зростає меншою мірою, ніж R². Крім того, може набувати й негативних значень, тоді як завжди позитивний. У прикладних задачах у випадках, коли виявляється негативним, його вважають таким, що дорівнює нулю. Для розглянутого нами прикладу кривої Філіпса маємо 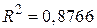, а .

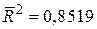Порівняння величин R²

У першу чергу дуже важливо відзначити, що при порівнянні моделей на основі значень коефіцієнтів детермінації, як нескоректованих, так і скоректованих, повинні бути однаковими об’єми вибірки N і одними й тими ж залежні змінні. Пояснювальні змінні можуть бути будь-якого вигляду. Так, для моделей

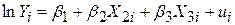;	(5.7.5)
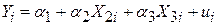
	(5.7.6)

не можна порівнювати підраховані . Причина полягає в тому, що за визначенням визначає частину дисперсії залежної змінної, поясненої за рахунок пояснювальних змінних, отже, в (5.7.5) виміряє частину в дисперсії 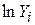, пояснену за рахунок Х₂ і Х₃, а в (5.7.6) це частина в дисперсії 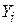, пояснена тими ж змінними. Зрозуміло, що це різні речі. Раніше ми відзначали, що змінювання 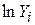дає відносне змінювання Y, тоді як змінювання Y є абсолютним змінюванням. Отже, 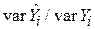не одне й те ж, що 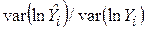. Тому коефіцієнти детермінації (5.7.5) і (5.7.6) не можна порівнювати.

Якщо ми звернемося до функції попиту на каву (2.7.1):

; , ; , , ; , ,

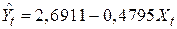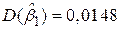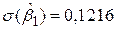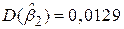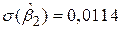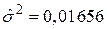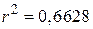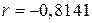що являє собою лінійну модель, і функції попиту (6.4.5):

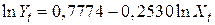R2=0,7448 (0,0152) (0,0494) F1,9=26,27 t = (51,0045) (–5,1251),

що представляє Log-Lin – модель, то порівнювати їх коефіцієнти детермінації безпосередньо не можна. Як же все-таки порівнювати величини для моделей вигляду (3.7.1) і (6.4.5)? Покажемо це на прикладі функції попиту на каву.

Для порівняння коефіцієнтів детермінації, отриманих із моделей із різним видом залежної змінної, як, наприклад, у моделях (3.7.1) і (6.4.5), можна застосувати два способи.

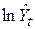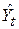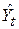1. За відомим значенням у моделі (6.4.5) знаходимо , а потім підраховуємо між і 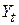за формулою (2.5.14):

.

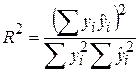Підрахований таким чином можна порівнювати з коефіцієнтом детермінації з моделі (6.4.5).

2. Підраховуємо за відомими 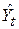з моделі (3.7.1) 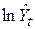і 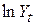, обчислюємо між ними. Цей коефіцієнт детермінації можна порівнювати з із моделі (6.4.5).

Припустимо, що ми спочатку вирішили порівнювати величину лінійної моделі (3.7.1) з величиною подвійної логарифмічної моделі (6.4.5). Використаємо значення 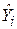моделі (3.7.1) і знайдемо за ними 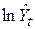, а потім за фактичними значеннями 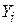знайдемо 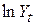. За отриманими значеннями 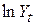і 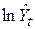ми можемо підрахувати , наприклад, за формулою

.

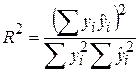Використовуючи дані, наведені в (5) і (6) стовпцях табл. 2.1, можна підрахувати за цією формулою величину . Отримуємо 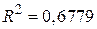. Цю величину вже можна порівняти зі значенням 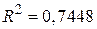з подвійної логарифмічної моделі. Порівняння цих величин виявляється на користь логарифмічної моделі.

Якщо ж ми хочемо порівняти величину із подвійної логарифмічної моделі з із лінійної моделі, то необхідно за значеннями 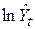з моделі (6.4.5) обчислити 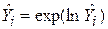, а потім за цими значеннями і 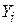обчислити . Використовуючи дані (4) і (1) стовпців табл. 2.1, знаходимо 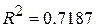. Це значення вже можна порівнювати зі значенням коефіцієнта детермінації з лінійної моделі 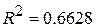. Як і раніше, подвійна логарифмічна модель має високий коефіцієнт детермінації.

На закінчення зробимо таке зауваження. Іноді дослідник прагне збільшити , тобто вибрати ту модель, яка має найвищий . Це не правильно, оскільки в регресійному аналізі нашою метою є не отримання за будь-яку ціну високого , а отримання надійних оцінок істинних коефіцієнтів популяцій регресії, що дають можливість зробити статистичні висновки. В емпіричному аналізі часто виникає ситуація, коли має високі значення, а при цьому деякі коефіцієнти регресії виявляються статистично незначущими або ж мають знак, протилежний очікуваному. Отже, дослідник повинен більше зосереджуватися на логічному або теоретичному зв’язку між пояснюваним і пояснювальними змінними та їх статистичній значущості. Якщо при цьому ми отримаємо високе значення , то тим краще. Однак, якщо малий, то це не означає, що наша модель обов’язково погана.