Нулевая и конкурирующая, простая и сложная гипотезы

Часто необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, но имеются основания предположить, что он имеет определенный вид (назовем его А), выдвигают гипотезу: генеральная совокупность распределена по закону А.

Таким образом, в этой гипотезе речь идет о виде предполагаемого распределения.

Возможен случай, когда закон распределения известен, а его параметры неизвестны. Если есть основания предположить, что неизвестный параметр 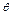равен определенному значению 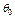, выдвигают гипотезу: 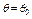. Таким образом, в этой гипотезе речь идет о предполагаемой величине параметра одного известного распределения.

Возможны и другие гипотезы: о равенстве параметров двух или нескольких распределений, о независимости выборок и многие другие.

Статистическойназывают гипотезу о виде неизвестного распределения, или о параметрах известных распределений.

Пример 9.1. Статистическими являются гипотезы:

1) генеральная совокупность распределена по закону Пуассона;

2) дисперсии двух нормальных совокупностей равны между собой.

В первой гипотезе сделано предположение о виде неизвестного распределения, во второй – о параметрах двух известных распределений.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине эти гипотезы целесообразно различать.

Нулевой (основной)называют выдвинутую гипотезу Но.

Конкурирующей (альтернативной) называют гипотезу Н₁, которая противоречит нулевой.

Например, если нулевая гипотеза состоит в предположении, что математическое ожидание а нормального распределения равно 10, то конкурирующая гипотеза, в частности, может состоять в предположении, что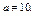

Коротко это записывают так: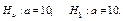

Различают гипотезы, которые содержат только одно и более одного предположений.

Простой называют гипотезу, содержащую только одно предположение.

Пример 9.2. Если 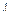– параметр показательного распределения, то гипотеза 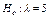– простая.

Сложнойназывают гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.

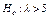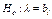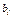Пример 9.3. Сложная гипотеза состоит из бесчисленного множества простых вида , где – любое число, большее 5.

В итоге проверки гипотезы могут быть допущены ошибки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута правильная нулевая гипотеза. Вероятность ошибки первого рода называют уровнем значимости и обозначают через .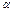

Ошибка второго рода состоит в том, что будет принята неправильная нулевая гипотеза. Вероятность ошибки второго рода обозначают через .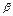

Статистическим критерием (или просто критерием) называют случайную величину К, которая служит для проверки гипотезы.

Наблюдаемым (эмпирическим) значением К_набл называют то значение критерия, которое вычислено по выборкам.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых нулевую гипотезу принимают.

Основной принцип проверки статистических гипотез: если наблюдаемое значение критерия принадлежит критической области, то нулевую гипотезу отвергают; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают.