Стискаюча функція на основі симетричного блокового алгоритму

В качестве сжимающей функции можно использовать симметричный блочный алгоритм шифрования. Для обеспечения большей безопасности можно использовать в качестве ключа блок данных предназначенный к хешированию на данной итерации, а результат предыдущей сжимающей функции в качестве входа. Тогда результатом последней итерации будет выход алгоритма. В таком случае безопасность хеш-функции базируется на безопасности используемого алгоритма.

Обычно при построении хеш-функции используют более сложную систему. Обобщенная схема симметричного блочного алгоритма шифрования изображена на рис.2

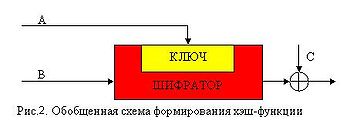
Вхідні параметри схеми шифрування A, B и C можуть отримувати значення M_i, H_i-1, (M_iÅH_i-1)або бути константою, де M_i ‑ i-й блок вхідного потоку, Å ‑ додавання за модулем 2, H_i ‑ результат i-ого циклу оброблення даних. Загалом можливо отримати 4х4х4=64 варіанти побудови стискаючої функції. Більшість з них є або тривіальними, або небезпечними. На рис. 3 зображені чотири найбільш безпечні схеми для відомих атак.

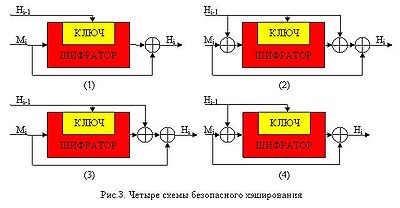
Зокрема, державний стандарт ГОСТ Р 34.11-94 фактично реалізує одну із зазначених схем побудови хеш-функцій.

Основним недоліком хеш-функцій, які побудовані на основі алгоритмів блокового шифрування, є вельми низка швидкість їх роботи. Математичні дослідження свідчать, що необхідна криптостійкість може бути забезпечена навіть в умовах меншої кількості операцій над вхідними даними.

Світові стандарти пропонують низку криптографічно стійких хеш-функцій, які не базуються на блокових алгоритмах шифрування та мають суттєво кращі швидкісні характеристики. Зокрема, до вказаної категорії слід віднести найбільш поширені стандарти хеш-функцій є MD5, RIPEMD-160, RIPEMD-256, SHA-1, SHA-2 що часто застосовуються, наприклад, у банківських захищених інформаційних технологіях.

Геш-функція 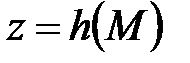- це перетворення бітового рядка 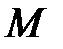довільної довжини у рядок (блок) 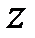фіксованої довжини 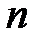(зазвичай, 160-512 битів), яке має наступні властивості.

Відновлення 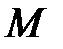виходячи із співвідношення 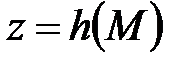, обчислювально неможливо.

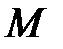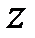За наявності и , обчислювально неможливо визначити другий прообраз для 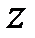, тобто повідомлення 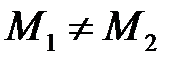, таке, що .

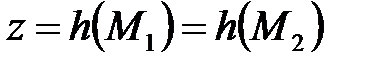На практиці, як правило? застосовуються геш-функції, що задовільняють більш жорстку умову: вимагається обчислювальна неможливість знаходження довільної колізії, тобто пари різних повідомлень 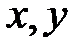, таких, що 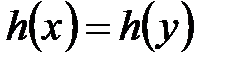. Подібні геш-функції називаються вільними від колізій.

Значення 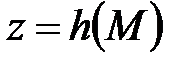називається геш-кодом повідомлення 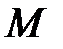, а величина 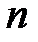- довжиною геш-коду.