Пример 2. Задача о ремонте.

Пусть при работе на некотором станке в течение недели будет получен доход Q = 100 р., а при выходе на этом отрезке времени станка из строя доход Q = 0 р. Если будет предварительно проведена профилактика, то вероятность выхода станка из строя равна q = 0,4,в противном случае, без профилактики эта вероятность равна q = 0,7.Стоимость профилактики 20 р.Целесообразно или не целесообразно проводить профилактику?

Рис. 6

Для решения этой задач методом динамического программирования построим дерево решения (рис. 6). На рисунке кружками показаны узлы (состояния системы), где решение принимает человек, квадратами — узлы, где решение носит вероятностный характер.

Анализ начинается с последнего этапа. На последнем этапе возможны 4-ре состояния. Соответствующий выигрыш W₃показан в кружках. Оценку 2-го этапа проведем по математическому ожиданию.

Для одного состояния эта оценка 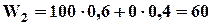, для другого 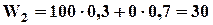. Эти оценки помещены в квадраты. Оценка последнего этапа (1-го по нумерации): в случае профилактики выигрыш равен W₁-= 60 — 20 = 40 р., без профилактики W₁ = 30 р. Решение: проводить профилактику W =40р.