Пример 3. Задача о выпуске партии консервов

Фирма освоила выпуск новых консервов. Образцы прошли дегустацию и сделан вывод, что при массовом выпуске консервов в производство успешный массовый сбыт ожидается с вероятностью 0,3, при этом ожидаемая годовая прибыль 3 млн. дол., а в случае неуспеха потери составят 250 тыс. дол. Возможен вариант предварительного пробного выпуска небольшой партии товара (затраты на выпуск партии составят 50 тыс. дол.). Оценки экспертов возможных ситуаций при продаже опытной партии и вероятности успеха и неуспеха при последующем массовом выпуске даны в таблице 6.

Итак, возможны решения.

1) Отказаться от выпуска.

2) Начать сразу массовый выпуск

3) Вначале выпустить опытную партию.

Необходимо построить дерево решений и, используя метод ДП, найти лучшее из возможных решение.

Табл. 6

События Результат массового выпуска	А) Покупают < 10% потребителей	Б) Покупают >10% вторично < 50%	В) Покупают >10% вторично >50%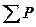
Успех	0,03	0,07	0,20	0,30
Неуспех	0,47	0,18	0,05	0,70
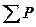
	0,50	0,25	0,25

Последовательно, начиная с последнего этапа, вычисляются условные оптимумы.

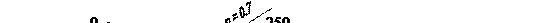
Рис 7

Дерево решений имеет вид, показанный на рис 7

1) Узлы (7),(8),(9). Чтобы подсчитать максимальные значения целевой функции на 1-м шаге, необходимо знать условные вероятности – условную вероятность события «У», если имело место событие «а» (успех при m₁<10%), p(У/a) и т.д.

Из таблиц п. 9.2. следует (решения «природы»).

p(У/a) = 0,03/0,5 = 0,06; p(НУ/a) = 0,47/0,5 = 0,94;

p(У/б) = 0,07/0,25 = 0,28; p(НУ/б) = 0,18/0,25 = 0,72;

p(У/в) = 0,20/0,25 = 0,8; p(НУ/в) = 0,05/0,25 = 0,2.

Соответствующие значения функций:

W₇ = 3000×0,06-250×0,94 = -55 тыс.

W₈ = 3000×0,28-250×0,72 = 660 тыс.

W₉ = 3000×0,8-250×0,2 = 2350 тыс.

2) Принимаются решения (условные оптимумы):

— узел 4 – «отказ», W₄ = 0.

— узел 5 – «МП», W₅ = 660 тыс.

— узел 6 – «МП», W₆ = 2350 тыс.

3) Узел 3. Решение «природы»

W₃ = 0×0,5+660×0,25+2350×0,25-50 = 702,5 тыс.

4) Узел 2. Решение «природы»

W₂ = 3000×0,3-250×0,7 = 725 тыс.

5) Узел 1. Выбор из трёх возможных решений делается в пользу массового производства W = 725 тыс. – наибольшая ожидаемая прибыль.

Можно отметить, что, если затраты на опытное производство будут менее 27,5 тыс., более выгодным окажется решение «начать с опытного производства».

ЛИТЕРАТУРА

1. Р. Акоф, М. Сасиени. Основы исследования операций. М., 1971.

2. Р. Акофф. Искусство решения проблем. М., 1982.

3. Бахвалов Н.С. Численные методы. М., 1975

4. С. Бир. Мы и сложность современного мира. Кибернетика сегодня: проблемы и суждения. М., 11.1976.

5. Блехман И.И., Мышкис А.Д., Пановко Я.Г. Механика и прикладная математика. Логика и особенности приложения математики. Киев, 1990.

6. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. М., 1980.

7. Гермейер Ю.Б. Введение в теорию исследования операций. М., 1971.

8. Грекова И. Методологические особенности прикладной математики на современном этапе её развития. //»Вопросы философии». 1976.6.

9. Грекова И. Всем ли ездить на ярмарку в Дублин? //»Знание — сила» 8. 1979.

10. Грекова И. Математика и постижение реальности. //»Наука и жизнь» 1985. 3.

11. Губанов В.А., Захаров В.В., Коваленко А.Н. Введение в системный анализ. Ленинград, 1988.

12. Дроздов Н.Д. Некоторые вопросы организации прикладных исследований. «Системы: Математические методы описания, САПР и управление». Калинин. 1989.

13. Дроздов Н.Д., Барсукова Н.Е. Динамика взаимодействия сельхозкооперативов и личных хозяйств членов этих кооперативов // Ученые записки Тверского университета. Тверь 1996.

14. Э.Квейд. Анализ сложных систем. М., 1969.

15. Клиланд Д., Кинг В. Системный анализ и управление.М.,1974.

16. Кравченко А.И. Прикладная социология и менеджмент. М.,1975.

17. Краснощеков П.С. Математические модели в исследовании операций. М., 1987.

18. Кудрявцев Л.Д. Мысли о современной математике и её изучении. М., 1977.

19. Моисеев Н.Н. Математик задает вопросы. М., 1974.

20. Моисеев Н.Н. Математик ставит эксперимент. М., 1979.

21. Моисеев Н.Н. Математические задачи системного анализа. М., 1981.

22. Моисеев Н.Н. Эффективность, устойчивость, справедливость.// «Знание — сила», 1984.3.

23. Моисеев Н.Н. Слово о научно-технической революции. М., 1985.

24. Э. Мушик, П. Мюллер. Методы принятия технических решений. М., 1990.

25. Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ. М., 1989.

26. Петров А.А., Поспелов И.Г., Шананин А.А. Опыт математического моделирования экономики.М.,1996.

27. Плотинский Ю.М. Математическое моделирование динамики социальных процессов. М., 1992.

28. П. Райветт, Р.Л. Акофф. Исследование операций. М., 1986.

29. Тихонов А.Н., Костомаров Д.П. Вводные лекции по прикладной математике. М., 1984.

30. Трухачев Р.И. Модели принятия решений в условиях неопределенностей. М., 1981.

31. Р. Шенон. Имитационное моделирование систем — Искусство и наука. М., 1978.

32. Исследование операций. под ред. Дж. Моудера, С. Элмаграби. М., 1981.

33. Эконометрическое моделирование. Ответственный редактор Иванилов Ю.П. М., 1992