Композиция оценок свойств и сравнение альтернатив.
Переход от сравнения отдельных свойств к сравнению альтернатив является задачей композиции. Возможны различные случаи решения этой задачи.
а) Случай, когда все свойства оценены численно — получен набор критериев.
Пусть Ck(ci) — численная оценка k-го свойства i-ой альтернативы,
k = 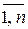 .
.
Введем векторное пространство, называемое критериальным, в котором каждой i-ой альтернативе будет соответствовать точка: C(ci) = {C1(ci), C2(ci),..., Cm(ci)}, т.е. k-ой составляющей вектораC(ci) является Ck(ci)- численная оценка k-го свойства i-ой альтернативы.
При сравнении двух альтернатив c1 и c2 альтернатива c1будет предпочтительнее альтернативе c2, если Ck(c1) ³ Ck(c2), для всех k= 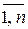 причем хотя бы одно неравенство строгое. Здесь и далее рассматривается случай, когда лучшему свойству соответствует большее значение численной оценки. В противном случае перед численными оценками свойств можно ставить знак «минус».
причем хотя бы одно неравенство строгое. Здесь и далее рассматривается случай, когда лучшему свойству соответствует большее значение численной оценки. В противном случае перед численными оценками свойств можно ставить знак «минус».
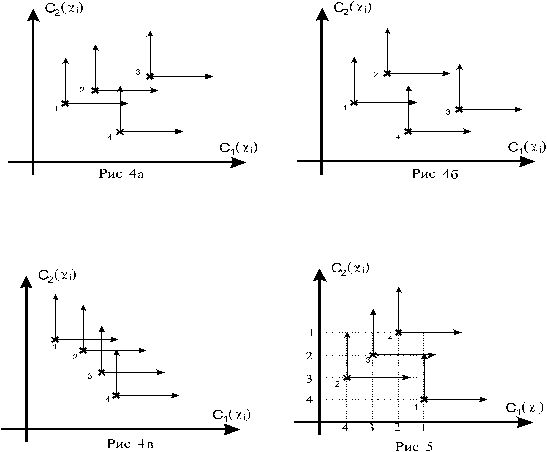
Поясним, как можно найти предпочтительные альтернативы, используя критериальное пространство. Рассмотрим для этого пример, когда альтернативы оцениваются по двум критериям. Принимая точку, соответствующую i-ой альтернативе, за начало координат, перенесем в эту точку все координатные оси критериального пространства. Если в положительном октанте полученной таким образом системе координат не окажется ни одной точки, соответствующей какой то другой альтернативе, то i-ая альтернатива является не улучшаемой.
На рис. 4а только одна неулучшаемая альтернатива — это альтернатива 3, на рис. 4б таких альтернатив две — 2 и 3, а на рис. 4в все альтернативы неулучшаемые.
Множество неулучшаемых альтернатив — это множество Парето. Получение множества Парето — 1-й шаг поиска лучшего решения. Есть много других, кроме рассмотренного, эффективных методов изучения множеств Парето.
Для выбора альтернативы на множестве Парето нужно привлекать другие соображения, связанные с особенностями решаемой задачи.
б) Случай, когда нет численных оценок, а есть только результаты попарного сравнения.
Пусть каждая альтернатива характеризуется n-свойствами и по каждому из этих свойств проведена операция пожарного сравнения. Все операции обладают свойствами транзитивности и антирефлексивности. Если сравнение возможно для каждой пары альтернатив по каждому свойству, то оказывается возможным все альтернативы ранжировать по каждому свойству, при этом будет получен набор перестановок из альтернатив — матрица с n-столбцами (по числу свойств) и m-строками (по числу альтернатив).
Пример. Пусть имеют место четыре альтернативы, каждая из которых характеризуется двумя свойствами. Результаты попарного сравнения имеют вид:
- по свойству 1: c1R1c4, c4R1c3, c3R1c2
- по свойству 2: c4R2c3, c3R2c2, c2R2c1
Соответственно матрица результатов сравнения имеет вид:
| Альтернативы | свойство 1 | свойство 2 |
| I | ||
| II | ||
| III | ||
| IV |
Один из способов дальнейшей работы с матрицей попарного сравнения — ввод условного векторного пространства свойств. Альтернативы располагаются на каждой из i-ых осей искусственно введенного критериального пространства в соответствии с их ранжированием по i-му свойству. Затем выделяются неулучшаемые альтернативы таким же способом, как в предыдущем случае.
Для приведенного выше примера 2-х альтернатив с 4-мя свойствами условное пространство свойств имеет вид, показанный на рис. 5.
В рассмотренном примере неулучшаемыми альтернативами являются 1 и 4.
После получения множества неулучшаемых альтернатив дальнейший выбор производится, как и в предыдущем случае, с учетом физической сущности процесса по какому либо правилу свертки множества критериев.
В рассмотренном примере в качестве лучшей может быть признана, например, альтернатива 4, у которой сумма рангов свойств наименьшая,
(2+1) < (1+4).
Более сложным является случай неполноты ранжирования.
5.3 Пример модели принятия решения
в условиях неопределенности
В условиях неопределенности принцип выбора зависит, как отмечалось выше, от характера противодействия противной стороны (внешней среды). В тех случаях, когда среда «ведет себя» антагонистическим образом по отношению к решению, выбранному органом управления системы, имеет место ситуация, относящаяся к теории игр. Если среда «пассивна» (например, это пассивная природа) и управляющему органу известно распределение вероятностей на множестве состояний среды, то имеет место «игра с природой» или «статистические решения». В общем случае возможна целая градация ситуаций, определяющих стратегию поведения среды.
Рассмотрим далее информационную ситуацию, когда распределения вероятностей на элементах состояния среды: априори известны. Рассмотрим простейший случай, не будем привлекать такие понятия как функция правдоподобия, функция потерь.
Итак, распределение вероятностей задано в виде ряда:
P= (p1,..,pj,.., pl ), pj= P(q=qj), 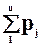 =1, где
=1, где  qj —состояние среды.
qj —состояние среды.
Это одна из возможных простейших ситуаций. На практике расчет априорного распределения вероятностей состояния среды производится либо путем обработки статистического материала, либо аналитическими методами на основании гипотез о поведении среды.
Обозначим.
1) c= {c1,..,ci,..,cm} — множество возможных альтернатив — вариантов принятия решения;
2)q={q1,..,qj,..,ql} — множество возможных состояний среды, причем вероятности этих состояний известны: Pj = P{q = qj};
3) Ф = {j1,..,jt,..,jr} —множество принципов (методов) выбора и оценки принятого решения;
С методом выбора решения связано понятие оценочного функционала — F.
F = {fi,j}, где fi,j — выигрыш (потеря), если при состоянии среды
qj Î qбыло принято решение ciÎc.
Будем считать, что оценочный функционал имеет положительный ингредиент и обозначается F+, если ставится задача достижения максимума: max{fi,j}. При отрицательном ингредиенте функционала F-лучшему решению соответствует min {fi,j}.
Таким образом ситуация принятия решения характеризуется тройкой {q,c,F}.
Соответственно, может быть получена матрица значений оценочного функционала (ситуационная матрица)
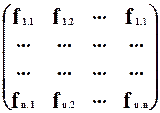
Различным принципам выбора соответствуют определенные критерии выбора – алгоритмы, которые определяют единственное оптимальное решение или множество таких решений. Для рассматриваемой ситуации могут быть использованы критерий Байеса, критерий минимакса (максимина), критерий минимума дисперсии оценочного функционала и др.
Рассмотрим эти подходы на примере.
Пусть оценочный функционал имеет положительный ингредиент, и ситуационная матрица имеет вид:
| q | q1 | q2 | q3 |
| R{q=qj} | 0.2 | 0.3 | 0.5 |
| c1 | |||
| c2 | |||
| c3 |
При использовании критерия Байесса максимизируется (в задаче на максимум) математическое ожидание результата. (Рассмотрен простой пример без использования решающих функций).
B*(P,ci)  =
= 
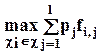
В рассматриваемом примере: В случае принятия альтернативы :
c1 — B*(P,c1) = 5·0,2 + 4·0,3 + 3·0,5 = 3,7.
c2 —B*(P,c2) = 4·0,2 + 5·0,3 + 5·0,5 = 4,2
c3 — B*(P,c3) = 4·0,2 + 2·0,3 + 4·0,5 = 3,4
Таким образом, согласно этому принципу наиболее предпочтительной является альтернатива c2.
При максминном подходе (в задаче на максимум) максимизируется наихудший из возможных результатов. (Здесь рассматриваются только чистые стратегии).
В*= 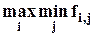
В рассматриваемом примере: в случае c1: min(5,4,3) = 3;
в случае c2: min(1,5,5) = 1;
в случае c3: min(4,2,4) = 2;
И согласно этому принципу наилучшей является альтернатива c1,которой соответствует максимум минимального результата.
Аналогично может быть решена задача на минимум.
В случае смешанных стратегий находится В*(ci,pi),отличающееся отнайденного вышеВ*.
5.4. Примеры решения оптимизационной задачи
методом динамического программирования
Динамическое программирование — метод оптимизации задач (процессов, операций), решение которых может быть разбито на несколько этапов, а целевая функция является, соответственно, аддитивной (или мультипликативной).
Пусть задача (процесс) разбита на nэтапов, 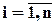 .
.
Целевая функция — суммарный выигрыш в задаче на максимум (суммарные потери в задаче на минимум) запишется в виде:



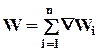 , где
, где 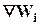 — выигрыш (потери) наi-мэтапе.
— выигрыш (потери) наi-мэтапе.
На каждом i-мэтапе система (процесс) может находиться в одном возможном для этого этапа состояний — ski, 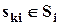 , здесь Si — множество всех состояний системы (процесса) на i-мэтапе. В каждом состоянии системы ski могут быть принято одно из возможных, согласно условиям задачи (операции), решений (управлений) — aj,ki, где
, здесь Si — множество всех состояний системы (процесса) на i-мэтапе. В каждом состоянии системы ski могут быть принято одно из возможных, согласно условиям задачи (операции), решений (управлений) — aj,ki, где 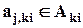 , здесь Aki — множество всех допустимых решений (управлений) при нахождении системы (процесса) на i-мэтапе в k-мсостоянии.
, здесь Aki — множество всех допустимых решений (управлений) при нахождении системы (процесса) на i-мэтапе в k-мсостоянии.
В результате принятия решения система (процесс) переходит в sl,i+1 состояние, при этом имеет место выигрыш (потери), равные 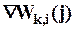 .
.
Таким образом, в результате принятия j-горешения система (процесс) перемещается с этапа iна этап i+1, при этом в зависимости от принятого решения переходит из состояния sk в состояние sl, а целевая функция получает приращение 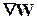 k,i(j).
k,i(j).
Существо метода заключается в том, что, начиная с последнего этапа, на каждом i-мэтапе для каждогоk-го состояния ищется так называемый условный оптимум W+k,i, являющийся суммой текущего приращения целевой функции и оптимального значения целевой функции от i+1 — гоэтапа до конца процесса
При этом. в результате управления, принятого на i-мэтапе, система (процесс) перейдет на i+1-мэтапе в состояние, зависящее от решения, принятого на i-мэтапе.
Основное рекуррентное соотношение метода запишется в виде:
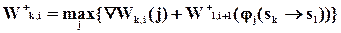 , где
, где 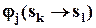 — функция, определяющая в какое состояние перейдет система (процесс) из состояния kна этапе iпри воздействие на систему управления aj,ki.
— функция, определяющая в какое состояние перейдет система (процесс) из состояния kна этапе iпри воздействие на систему управления aj,ki.
После последовательного вычисления всех условных оптимумов от последнего n-го этапа до 1-гобудет получен абсолютный оптимум и определен вектор управлений Aопт = (a1, a2,…,aj,ki,…,an), обеспечивающий этот оптимум.
Дата добавления: 2020-11-18; просмотров: 681;











