Пример 1. Задача о размещении инвестиций

Пусть сумма в 5 млрд. может быть вложена (инвестирована) в четыре предприятия. Эта сумма может быть разделена произвольно с дискретностью в 1 млрд. Ожидаемая прибыль (дивиденды) 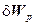в зависимости от суммы вложения для каждого p-го предприятия показана в табл. 1.

Табл.1

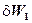
	0		9	12	14	16
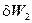
	0	4	10	13	14	15
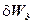
	0	3	7	11	15	17
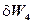
	0	6	11	12	13	14

Из данных таблицы следует, что инвестиция в 1 млрд. в предприятие 1 даст прибыль в 5 млн., в пр. 2 — 4 млн., в пр. 3 — 3 млн., в пр. 4 — 6 млн. Аналогично интерпретируются данные остальных столбцов таблицы. Необходимо так распределить 5 млрд., чтобы получить максимум суммарной прибыли.

В этой задаче в терминах динамического программирования этапами является выделение определенной суммы очередному предприятию, состояние системы — размер суммы, которая делится между очередным предприятием и остальными, управление — решение о разделе суммы. Поскольку здесь номер предприятия условен на конечном этапе можно рассмотреть любое предприятие. Пусть это будет предприятие №1.

Для конечного 4-го этапа (нумерация этапов ведется от начала процесса) возможны шесть состояний: осталось для выделения 1-му предприятию 0, 1, 2, 3, 4, 5 млрд. Управление единственное для каждого состояния — оставшаяся сумма передается предприятию №1. Полученная прибыль приведена в табл. 2.

Табл.2

На этапе 3 производится распределение средств между 1-м и 2-м предприятиями. Возможны те же шесть состояний, что и в предыдущем случае, однако для каждого состояния возможны шесть решений: 2-му предприятию выделяется 0, 1, 2, 3, 4, 5 млрд., соответственно. Результаты распределения показаны в табл.3.

Поясним, как заполняется табл.3. Состояние системы определено в верхней строчке таблицы, управление — в левом столбце. Пусть система находится в состоянии 3 (делится 3 млрд.) и принято решение о выделении предприятию 2 двух млрд. Тогда прибыль от 2-х млрд. составит 10 млн., оставшейся 1млрд. передается предприятию 1 и даст прибыль в 5 млн.

Суммарная прибыль при таком решении о распределении 3 млрд. составит 15 млн., что и показано в таблице. Для каждого состояния системы определяется решение, обеспечивающее максимум прибыли. Соответствующие цифры выделены в столбцах и перенесены на последнюю строчку.

Табл.3

	0		9	12	14	16
	-	4	9	13	16	18
	-	-
	-	-	-	13	18	21
	-	-	-	-	14	19
	-	-	-	-	-	15

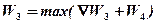
Таким образом, получен результат оптимального распределения средств между 1-м и 2-м предприятиями, т.е. получены условные оптимумы для 3-го этапа.

Информация относительно следующего 2-го этапа содержится в табл.4.

Табл.4

	-	3	8	13	18
	-	-	7	12	17
	-	-	-	11	16	21
	-	-	-	-	15	20
	-	-	-	-	-	17

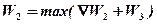
На этом этапе происходит распределение вложений между 1, 2 и 3 предприятиями. Состояний системы по-прежнему шесть (верхняя строка таблицы). Управление для каждого состояния заключается в выделении 3-му предприятию от 0 до 5 млрд. (левый столбец таблицы). При выделении какой либо суммы 3-му предприятию результат оптимального распределения остатка между 1 и 2 предприятиями берется из последней строки таблицы 3. Например, в состоянии 4 (делятся 4 млрд.) принимается решение выделить 3-му предприятию 1 млрд., что обеспечит прибыль в 3 млн., распределение оставшихся 3-х млрд. даст прибыль в 15 млн. Суммарный результат в таблице — 18 млн. Максимизируя прибыль для каждого состояния системы (по столбцам), получим на последней строчке таблицы результат оптимального распределения выделяемой суммы между 1, 2 и 3 предприятиями (условные оптимумы для каждого состояния системы).

Последний (1-ый с начала нумерации) этап. Состояние системы одно — распределяется вся сумма. Управление заключается в том, какую часть этой суммы выделяется 4-му предприятию. Результат оптимального распределения остатка берется из последней строки таблицы 4. Информация относительно 1-го этапа содержится в табл.5

Как следует из анализа табл. 5, максимальная прибыль в 26 млн. будет получена при выделении 4-му предприятию 2 млрд. Чтобы выяснить, как при этом должна распределяться оставшаяся сумма в 3 млрд., возвратимся назад последовательно к таблицам 4, 3, 2.

Табл.5

	22
	25
	22
	18
	14

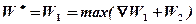
Из табл. 4 следует, что для состояния 3 оптимум будет получен, если 3-му предприятию ничего не выделяется, т.е. сохраняется состояние 3. Переходим к табл. 3.

Из табл. 3 следует, что при разделении 3 млрд. между 1 и 2 предприятиями необходимо для получения оптимальной прибыли 2-му выделить 2 млрд., 1-му — 1 млрд.

Таким образом, оптимальное управление обеспечивается вектором (1, 2, 0, 2),что соответствует прибыли в 26 млн. Действительно, если обратиться для проверки к таблице 1, получим, что выделение предприятиям 1, 2, 3, 4, соответственно 1, 2, 0, 2 млрд. даст суммарную прибыль 5+10+0+11=26 млн.

В предыдущем примере рассмотрен детерминированный вариант задачи, т.е. такой случай, когда все решения принимает человек. В стохастическом варианте задачи решения на определенных этапах носят случайный характер и их результаты могут быть осмыслены с помощью вероятностных оценок. Рассмотрим соответствующие примеры.