Измерительные шкалы

При проведении исследований всегда необходимо точно представлять, какая измерительная шкала может быть использована при измерении (оценке) наблюдаемых величин, (явлений, процессов, объектов).

Измерение — это операция, которая ставит в соответствие наблюдаемому явлению определенные обозначения: числа, номера, символы. При этом должны быть соблюдены следующее условие: различным состояниям явления соответствуют различные обозначения, не различным — одинаковые.

В зависимости от вида (характера) измеряемого явления используются следующие шкалы.

1) Шкала наименований (номинальная, классификационная).

Существует конечное число классов эквивалентности явлений (объектов). Каждому классу присваивается свое обозначение. Измерение заключается в определение, к какому классу относится объект. Возможна иерархия классов. Характерный пример иерархии классов — почтовые адреса. Данные в номинальных шкалах — всегда только символы, если это даже цифры. Единственная допустимая операция — проверка совпадения, для чего введен символ Кронекера — d_ij.

d_ij =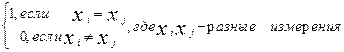

На этой основе возможны более сложные операции:

- количество совпадений: n_i = ;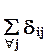

- относительная частота класса: 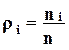, здесь n-общее число
измерений;

- различные статистические процедуры;

2) Порядковые (ранговые) шкалы.

Используются для сравнения объектов, классов по каким либо признакам, качествам. Пример — шкала родственных отношений:

отец = мать > сын = дочь;

дядя = тетя < брат = сестра.

В порядковых шкалах справедливо:

если А > В, то В < А ;

если А > В, В > С, то А > С.

Понятия дистанции межу шкалами нет. Для сравнения вводится ранг R_i —ранг i-го объекта:

R_i= 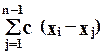,гдес(t)= 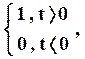_{i=Î(1,2,...,n),}

т.е. c(t) — индикатор положительности чисел.

Используется также и символ Кронекера.

3) Модифицированные ранговые шкалы.

Эти шкалы имеют место при арифметизации качественных измерений.

Примеры таких шкал.

а) Шкала твердости по Мозесу.

1 — тальк, 2 — гипс, 3 — кальций, 4 — флюорит, 5 — апатит,

6 — ортоклаз, 7 — кварц, 8 — топаз, 9 — корунд, 10 — алмаз.

Здесь не означает, что разность по твердости между корундом и алмазом такая же как, например, между тальком и гипсом.

б) Шкала силы ветра по Бофорту.

в) Шкала землетрясений по Рихтеру.

г) Бальные шкалы оценки знаний.

д) Порядковые шкалы Акоффа-Черчмена для упорядочения альтернатив с учетом силы предпочтения.

4) Шкалы интервалов.

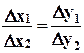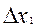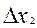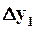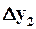Проводится упорядочение объектов с точностью до интервалов между ними. Единицы измерений произвольны, но постоянны по всей шкале, т.е. при произвольном выборе 0 и 1 справедливо , где и — расстояния между объектами в одной шкале, а и — расстояния между теми же объектами в другой шкале.

Таким образом, связь между шкалами линейная y = ax + b, a > 0, - 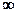<b<+ .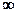

Имеют смысл только действия над интервалами, а не над отсчетами шкал. Возможны любые арифметические операции. При статистических оценках центральные моменты имеют смысл, а начальные — нет, поэтому не имеет смысла и коэффициент вариации.

5) Шкалы отношений.

Измерения являются полноправными числами. 0 — единственный.

Для двух шкал отношений справедливо 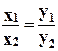, и, где x₁ и x₂ измерения в одной шкале, а y₁ и y₂ — измерения тех же величин в другой шкале.

Соответственно справедливо: y = ах, a > 0.

Примеры: шкалы измерения длин, весов, денег.

6) Шкалы разностей (периодические, циклические).

Шкалы инвариантны к сдвигу на некоторую постоянную (период).

Справедливо y = x + b, b — постоянная величина.

0 здесь условен, иначе это шкала интервалов. При вводе условного нуля возможны арифметические действия.

Примеры: — шкалы часов, компаса.

7) Абсолютная шкала.

0 и 1 — зафиксированы. Единица измерения безразмерна. Эта числовая шкала может быть как самостоятельной, так и вспомогательной для других шкал.

8) Шкалы размытых множеств.

Размытое множество A это совокупность упорядоченных пар вида A = {x, m_А(x)},гдеm_А(x) — функция принадлежности x множеству A, 0 £ m_А(x) £ 1.

Для уяснения особенностей построения шкал размытых множеств необходимо обратиться к алгебре размытых множеств, а для построения самих шкал нужно ввести ряд дополнительных определений. /25/

Перевод полученных измерений в другую более сильную шкалу возможен, но требует аккуратности.