Криволинейное движение. Тангенциальное и нормальное ускорения
Рассмотрим движение материальной точки по криволинейной плоской траектории. Вектор скорости в любой точке траектории направлен по касательной к ней.
Допустим, что в точке 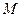 траектории вектор скорости был равен
траектории вектор скорости был равен 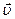 , а в точке
, а в точке 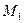 стал
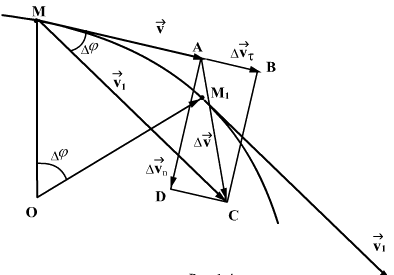
стал 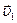 (рис. 1.6.1).
(рис. 1.6.1).
|
| Рис. 1.6.1 |
Для того, чтобы найти вектор изменения скорости 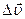 , необходимо из вектора
, необходимо из вектора 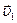 вычесть вектор
вычесть вектор 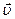 :
:
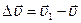 .
.
Для этого перенесем 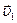 параллельно самому себе, совмещая его начало с точкой
параллельно самому себе, совмещая его начало с точкой 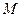 . Разность двух векторов равна вектору
. Разность двух векторов равна вектору 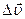 , проведенному из конца вычитаемого к концу уменьшаемого вектора. Модуль вектора
, проведенному из конца вычитаемого к концу уменьшаемого вектора. Модуль вектора 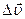 равен длине отрезка
равен длине отрезка 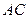 .
.
Разложим вектор 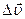 на два составляющих вектора
на два составляющих вектора 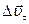 и
и 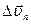 , модули которых равны соответственно
, модули которых равны соответственно 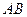 и
и 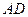 .
.
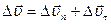
По определению
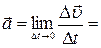 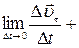 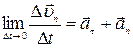
| (1.6.1) |
Тангенциальное ускорение 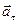 характеризует быстроту изменения модуля мгновенной скорости.
характеризует быстроту изменения модуля мгновенной скорости.
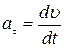 . .
| (1.6.2) |
Вектор 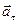 направлен по касательной к траектории в сторону вектора скорости, если
направлен по касательной к траектории в сторону вектора скорости, если 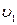 ˃
˃ 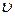 , и в сторону, противоположную вектору скорости, если
, и в сторону, противоположную вектору скорости, если 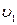 <
< 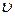 .
.
Нормальное ускорение 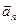 характеризует быстроту изменения направления вектора мгновенной скорости.
характеризует быстроту изменения направления вектора мгновенной скорости.
Вычислим модуль вектора 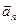 . Для этого проведем перпендикуляры через точки
. Для этого проведем перпендикуляры через точки 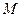 и
и 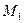 к касательным к траектории (рис. 1.6.1)
к касательным к траектории (рис. 1.6.1) 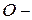 точка пересечения перпендикуляров. При достаточно малом
точка пересечения перпендикуляров. При достаточно малом 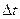 участок криволинейной траектории можно считать частью окружности радиуса
участок криволинейной траектории можно считать частью окружности радиуса 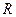 , называемого радиусом кривизны траектории в окрестностях данной точки. Треугольники
, называемого радиусом кривизны траектории в окрестностях данной точки. Треугольники 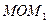 и
и 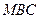 подобны, потому, что являются равнобедренными треугольниками с одинаковыми углами при вершинах.
подобны, потому, что являются равнобедренными треугольниками с одинаковыми углами при вершинах.
Поэтому:
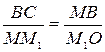 ,
,
или
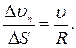
Но
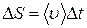 ,
,
тогда:
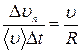 .
.
Переходя к пределу при 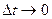 и учитывая, что при этом
и учитывая, что при этом 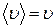 , находим:
, находим:
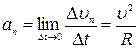 . .
| (1.6.3) |
Так как при 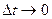 угол
угол 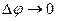 , направление вектора
, направление вектора 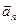 совпадает с направлением нормали к вектору скорости
совпадает с направлением нормали к вектору скорости 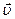 , т.е. вектор
, т.е. вектор 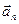 перпендикулярен к вектору
перпендикулярен к вектору 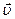 .
.
В случае движения тела по окружности нормальное ускорение 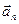 называют центростремительным.
называют центростремительным.
|
| Рис. 1.5 |
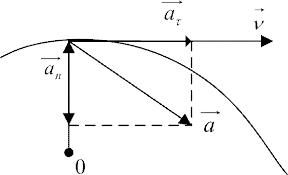
Вектор полного мгновенного ускорения 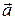 определяется векторной суммой тангенциального нормального ускорений (1.6.1).
определяется векторной суммой тангенциального нормального ускорений (1.6.1).
Так как векторы этих ускорений взаимно перпендикулярны, то модуль полного ускорения равен
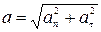
| (1.6.4) |
Направление вектора полного ускорения определяется углом 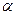 между векторам
между векторам 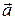 и
и 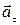 :
:
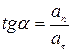 .
.
Проанализируем некоторые частные случаи движения:
а) 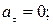
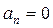 .
.
Так как 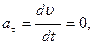 то
то 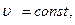 значит, движение равномерное.
значит, движение равномерное.
Если 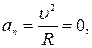 при
при 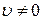 , то R
, то R 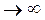 , значит, траектория движения - прямая линия. Таким образом, в этом случае движение материальной точки прямолинейное равномерное.
, значит, траектория движения - прямая линия. Таким образом, в этом случае движение материальной точки прямолинейное равномерное.
б) 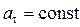 ,
, 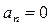 .
.
Если 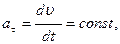 то за равные промежутки времени скорость изменяется на одинаковую величину, значит, движение равнопеременное. При
то за равные промежутки времени скорость изменяется на одинаковую величину, значит, движение равнопеременное. При 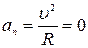 траектория движения представляет собой прямую линию. Таким образом, в данном случае материальная точка совершает прямолинейное равнопеременное движение.
траектория движения представляет собой прямую линию. Таким образом, в данном случае материальная точка совершает прямолинейное равнопеременное движение.
в) 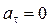 ,
, 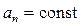 .
.
Если 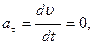 то движение равномерное. При
то движение равномерное. При 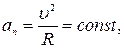
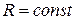 , траектория движения - окружность. Значит, в данном случае материальная точка совершает равномерное движение по окружности.
, траектория движения - окружность. Значит, в данном случае материальная точка совершает равномерное движение по окружности.
г) 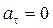 ,
, 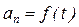 .
.
Если 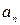 является функцией времени, то движение криволинейное. Так как
является функцией времени, то движение криволинейное. Так как 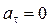 , то движение равномерное. Таким образом, в этом случае материальная точка совершает равномерное криволинейное движение.
, то движение равномерное. Таким образом, в этом случае материальная точка совершает равномерное криволинейное движение.
д) 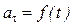 ,
, 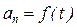 .
.
Если и тангенциальное, и нормальное составляющие ускорения являются функциями времени, то движение неравномерное криволинейное.
Дата добавления: 2016-10-07; просмотров: 3109;











