Нормальное и касательное напряжение, действующие в движущейся жидкости

Закон сохранения количества движения для неизолированной системы может быть записан в виде:

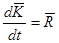
где 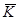- главный вектор количества движения системы

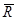- главный вектор внешних сил, действующих на систему

В жидкости выделим элементарный тетраэдр с гранями 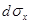, , 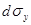, 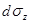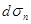. Индекс показывает перпендикулярно какой оси расположены грани, 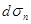- наклонная грань. К граням приложены соответствующие напряжения 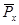, , 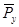, 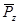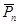(не перпендикулярные граням). Масса тетраэдра 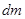. На тетраэдр действуют массовые и поверхностные силы. Массовые характеризуются вектором плотности 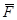, поверхностные – напряжениями.

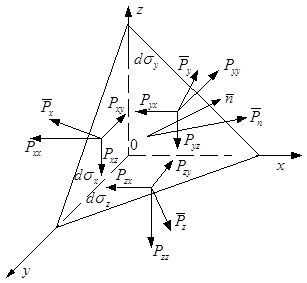
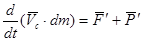
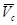- скорость центра инерции тетраэдра

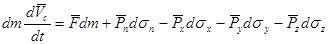
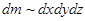- третий порядок малости

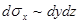- второй порядок малости

Членами третьего порядка малости пренебрегаем.

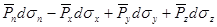
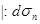
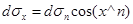и т.д.

п_х

Получим связь напряжений, действующих на грани выделенного тетраэдра:

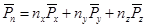
В проекциях на координатные оси это уравнение может быть переписано:

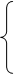
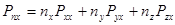
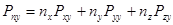
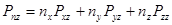
В записанной системе 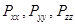называются нормальными напряжениями, а 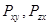и т.д. называются касательными напряжениями. Все напряжения могут быть записаны в матричной форме в виде симметричного тензора напряжений:

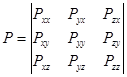
Первый индекс определяет ось, относительно которой расположена грань, второй – ось на которую проецируется напряжение.