Геометрическое распределение.
Системы (*) и (**) (см. прошлую лекцию) определяют функцию распределения времени выполнения команды в устройстве. В этом случае граф переходов будет очень сложным и определить в явном виде вероятности простоя сложно. Если мы зададим функцию распределения более упрощенно, то мы продвинемся в решении задачи. В связи с выше сказанным введем для описания времени выполнения команды в устройстве геометрический закон распределения.
Геометрическое распределение характеризуется двумя параметрами периодом (t) и вероятностью (p) повторения данного периода.

|
Посмотрим, как геометрическое распределение вводится для нашего случая: с вероятностью 1-p время выполнения команды равно t; с вероятностью (1-p)p время выполнения равно 2t; и т.д. с вероятностью (1-p)pi-1 время выполнения команды равно it. Таким образом в конце любого периода с вероятностью p команда продолжает выполнятся, а с дополнительной вероятностью (1-p) закончит свое выполнение.
Пример.

|
Определим состояние системы тремя параметрами U1U2U3, где U1 - указывает сколько времени осталось до завершения считывания команды из ОП; U2 - количество команд в буфере; U3 - показывает выполняется (1) или не выполняется (0) команда в ЦП.
Построим граф переходов данной системы.
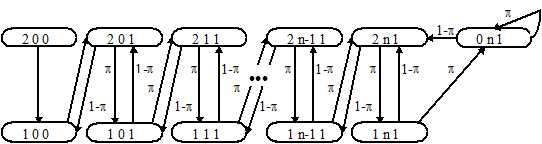
|
Составим систему уравнений
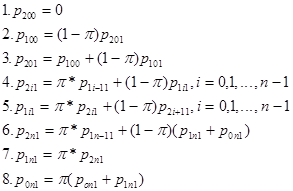
В данной системе одно уравнение линейно зависимо, следовательно надо отбросить любое уравнение и добавить уравнение нормировки. Решается эта система любым из известных способов.
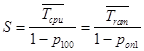
Найдем  цп
цп
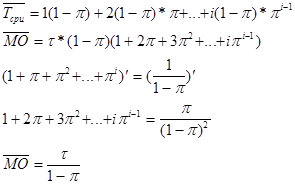
Лекция №7.
Дата добавления: 2016-11-04; просмотров: 1621;











