Локальная теорема Лапласа
Пользоваться формулой Бернулли при больших значениях п достаточно трудно, так как формула требует выполнения действий над громадными числами.
Например, если п = 50, k = 30, р = 0,1, то для отыскания вероятности 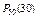 надо вычислить выражение
надо вычислить выражение 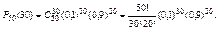
где 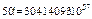 ,
,
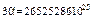 ,
,
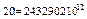 .
.
Правда, можно несколько упростить вычисления, пользуясь специальными таблицами логарифмов факториалов. Однако и этот путь остается громоздким и к тому же имеет существенный недостаток: таблицы содержат приближенные значения логарифмов, поэтому в процессе вычислений накапливаются погрешности; в итоге окончательный результат может значительно отличаться от истинного.
Естественно возникает вопрос: нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли?
Оказывается, можно. Локальная теорема Лапласа и дает формулу, которая позволяет приближенно найти вероятность появления события ровно k раз в п испытаниях, если число испытаний достаточно велико.
Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 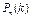 того, что событие А появится в п испытаниях ровно k раз, приближенно равна (тем точнее, чем больше п) значению функции
того, что событие А появится в п испытаниях ровно k раз, приближенно равна (тем точнее, чем больше п) значению функции
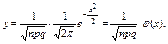
при 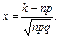
Имеются таблицы (Приложение 1), в которых помещены значения функции 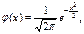 соответствующие положительным значениям аргумента х. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция
соответствующие положительным значениям аргумента х. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция 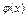 нечетна, т. е.
нечетна, т. е.
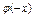 = –
= – 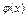 .
.
Итак, вероятность того, что событие А появится в п независимых испытаниях ровно k раз, приближенно равна:
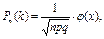
где 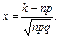
Пример 3.4. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение.
По условию, n = 400; k = 80; р = 0,2; q = 1 – 0,8.
Воспользуемся формулой Лапласа:
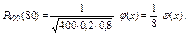
Вычислим определяемое данными задачи значение х:
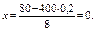
По таблице находим 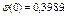
Искомая вероятность
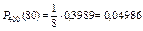
Дата добавления: 2016-07-27; просмотров: 1684;











