Арифметические операции над функциями. Композиция функций
Определение 1. Пусть функции f и g заданы на множестве 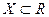 . Суммой функций f и g называется функция
. Суммой функций f и g называется функция 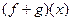 , значение которой в точке
, значение которой в точке 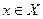 определяется как сумма значений функций f и g в этой точке, то есть
определяется как сумма значений функций f и g в этой точке, то есть
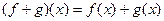 .
.
Аналогично определяется разность
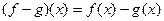 ,
,
Произведение
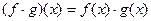 ,
,
частное функций, если 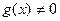 ,
,
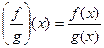 .
.
Определение 2. Пусть действительная функция f задана на множестве Х, а действительная функция g – на множестве 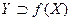 . Тогда существует композиция отображений
. Тогда существует композиция отображений 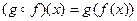 , которая является действительной функцией, заданной на множестве Х и называемой композицией действительных функций f и g или сложной функцией.
, которая является действительной функцией, заданной на множестве Х и называемой композицией действительных функций f и g или сложной функцией.
Заметим, что сложную функцию 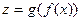 можно записать в виде цепочки функций
можно записать в виде цепочки функций 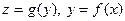 . Переменную у в этом случае обычно называют промежуточной переменной. Заметим также, что термин «сложная функция» характеризует не сложность функции, а способ ее задания. Например, функция
. Переменную у в этом случае обычно называют промежуточной переменной. Заметим также, что термин «сложная функция» характеризует не сложность функции, а способ ее задания. Например, функция 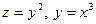 или
или 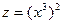 - сложная функция, а тождественная ей функция
- сложная функция, а тождественная ей функция 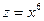 уже не является сложной.
уже не является сложной.
Пример 1. Если 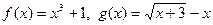 , то
, то 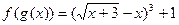 ,
, 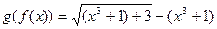 .
.
Может получиться так, что множество 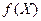 не является подмножеством множества Y. В этом случае сложная функция определена лишь для тех х, для которых
не является подмножеством множества Y. В этом случае сложная функция определена лишь для тех х, для которых 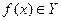 .
.
Пример 2. Пусть 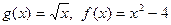 . Тогда
. Тогда 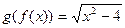 . Здесь
. Здесь 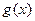 задана на множестве
задана на множестве 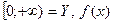 задана на
задана на 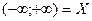 и
и 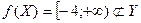 . Сложная функция
. Сложная функция 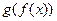 рассматривается для х таких, что
рассматривается для х таких, что 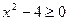 , то есть
, то есть 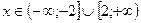 .
.
Пример 3. Функции 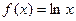 и
и 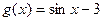 не определяют функции
не определяют функции 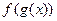 , так как
, так как 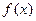 определена для
определена для 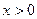 , а
, а 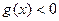 для всех
для всех 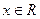 .
.
Пример 4. (Решить самостоятельно). Пусть 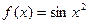 и
и 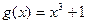 . Найти следующие функции и указать их области определения:
. Найти следующие функции и указать их области определения: 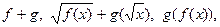
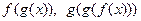 .
.
Дата добавления: 2016-06-09; просмотров: 9615;











