Повторные испытания
3.1. Формула Бернулли.
3.2. Локальная теорема Лапласа.
3.3. Интегральная теорема Лапласа.
Формула Бернулли
Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся считать, что вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q = 1– р.
Поставим перед собой задачу вычислить вероятность того, что при п испытаниях событие А осуществится ровно k раз и, следовательно, не осуществится п – k раз.
Важно подчеркнуть, что не требуется, чтобы событие А повторилось ровно k раз в определенной последовательности.
Пример 3.1. Если речь идет о появлении события А три раза в четырех испытаниях, то возможны следующие сложные события:
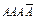 ,
, 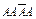 ,
, 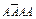 ,
, 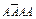 .
.
Искомую вероятность обозначим Рп(k).
Пример 3.2. Символ 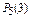 означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза.
означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза.
Поставленную задачу можно решить с помощью так называемой формулы Бернулли.
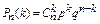
или
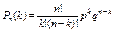 .
.
Пример 3.3. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна р = 0,75.
Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение.
Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна р = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1 – 0,75 = 0,25.
Искомая вероятность по формуле Бернулли равна:
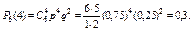
Дата добавления: 2016-07-27; просмотров: 2302;











