Закон Био-Савара-Лапласа и его применение для расчета магнитных полей.

Магнитное поле постоянных токов различной формы было подробно исследовано фр. учеными Био и Саваром. Ими было установлено, что во всех случаях магнитная индукция в произвольной точке пропорциональна силе тока, зависит от формы, размеров проводника, расположения этой точки по отношению к проводнику и от среды.

Результаты этих опытов были обобщены фр. математиком Лапласом, который учел векторный характер магнитной индукции и высказал гипотезу о том, что индукция 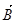в каждой точке представляет собой, согласно принципу суперпозиции, векторную сумму индукций 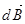элементарных магнитных полей, создаваемых каждым участком этого проводника.

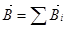или .

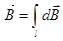Лапласом в 1820 г. был сформулирован закон, который получил название закона Био-Савара-Лапласа: каждый элемент 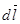проводника с током 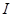создает магнитное поле, вектор индукции которого 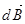в некоторой произвольной точке К определяется по формуле:

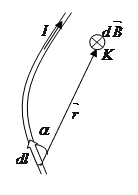
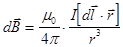- закон Био-Савара-Лапласа.

Из закона Био-Совара-Лапласа следует, что направление вектора 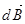совпадает с направлением векторного произведения 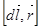. Такое же направление дает и правило правого винта (буравчика).

Учитывая, что ,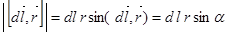

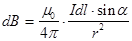
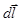- элемент проводника, сонаправленный с током;

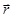- радиус-вектор, соединяющий 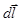c точкой K;

a - угол между 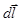и .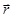

Закон Био-Савара-Лапласа имеет практическое значение, т.к. позволяет найти в заданной точке пространства индукцию магнитного поля тока, текущего по проводнику конечный размеров и произвольной формы.

Для тока произвольной формы подобный расчет 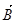представляет собой сложную математическую задачу. Однако, если распределение тока имеет определенную симметрию, то применение принципа суперпозиции совместно с законом Био-Савара-Лапласа дает возможность относительно просто рассчитать конкретные магнитные поля.

Рассмотрим некоторые примеры.

А. Магнитное поле прямолинейного проводника с током.

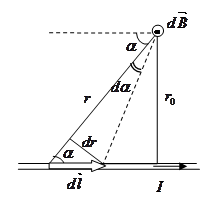
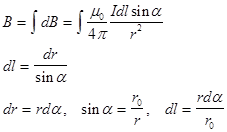
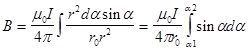
1) для проводника конечной длины:

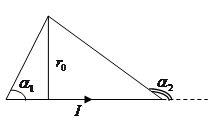
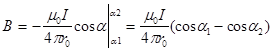
2) для проводника бесконечной длины: a₁ = 0, a₂ = p

.

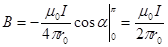Б. Магнитное поле в центре кругового тока:

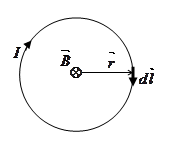
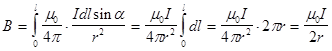
a=90⁰, sina=1,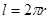

3. Теорема о циркуляции вектора 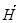(закон полного тока) и ее применение для расчета магнитных полей.

Эрстедом в 1820 году экспериментально было обнаружено, что циркуляция 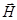по замкнутому контуру, окружающему систему макротоков, пропорциональна алгебраической сумме этих токов. Коэффициент пропорциональности зависит от выбора системы единиц и в СИ равен 1.

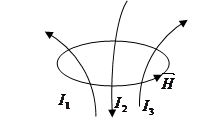Циркуляцией вектора 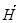называется интеграл по замкнутому контуру.

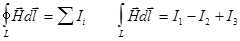
Эта формула носит название теоремы о циркуляции 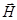или закона полного тока:

циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру равна алгебраической сумме макротоков (или полному току), охватываемых этим контуром.

Если, кроме токов проводимости, есть еще ток смещения (переменное электрическое поле), то и его надо включить в сумму токов.

а) поле прямолинейного бесконечного проводника с током:

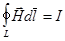- согласно теореме о циркуляции.

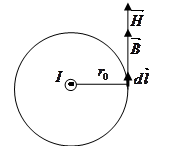
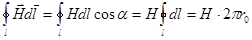
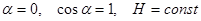- на окружности

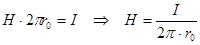
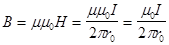- т.к. m = 1 - для воздуха

б) поле внутри длинного соленоида с током.

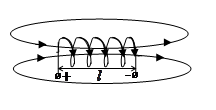Каждая силовая линия проходит обязательно как внутри соленоида, так и вне его. Подавляющее число линий вне соленоида проходит на расстоянии от него порядка длины соленоида l. Если длина соленоида во много раз больше его радиуса, то поле вне соленоида пренебрежимо мало по сравнению с полем внутри него.

Ø

Если

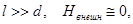
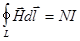
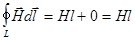
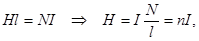
B=mm₀H=mm₀nI

где 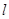- длина соленоида;

N - число витков;

n - число витков на единице длины.

в) поле тороида.

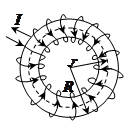
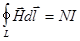
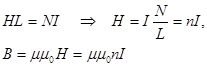
L - длина средней линии тороида.