ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ ТЕЛА

Деформированное состояние тела в точке тела описывается симметричным тензором деформаций

,

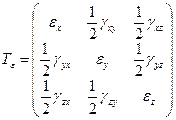где 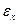, , 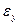, , 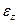, 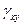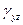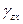- линейные и угловые деформации соответственно.

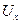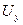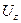Компоненты малых деформаций вычисляются через перемещения , и в декартовой системе координат по формулам

; ;

; ;

;

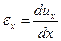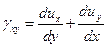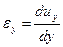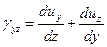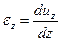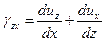
и удовлетворяют условиям неразрывности деформаций

;

;

;

;

;

.

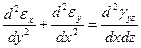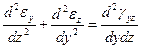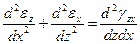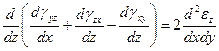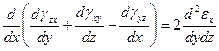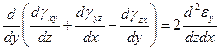С геометрической точки зрения эти соотношения являются условиями, определяющими деформацию, при которой тело остается сплошным.

Во всех точках деформационного тела существуют взаимно перпендикулярные оси, для которых компоненты угловой деформации равны нулю. Эти оси называются главными осями деформации. Материальные волокна, выбранные вдоль них, после деформации остаются взаимно перпендикулярными и имеют экстремальные удлинения.

Величины главных линейных деформаций 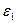, , 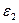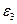определяются из решения кубического уравнения

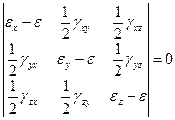
или

,

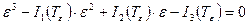где 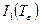, , 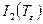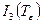- инварианты тензора малых деформаций.

В произвольной системе координат они имеют следующие значения:

,

,

,

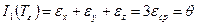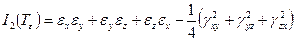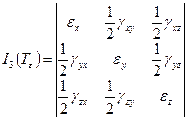где 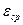- средняя деформация, 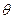- объемная деформация,

.

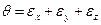В главных осях тензор деформаций имеет вид .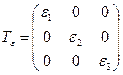

При разложении тензора деформаций на шаровой и девиатор их компоненты связаны следующим образом:

.

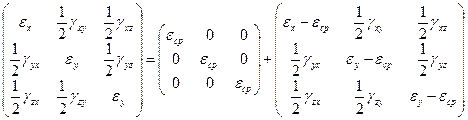Ориентация главных осей деформаций относительно системы координат , , 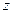определяется направляющими косинусами, величины которых рассчитываются из следующей системы уравнений

,

,

,

.

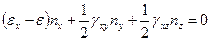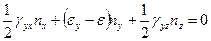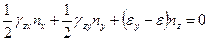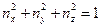Важную роль в теории деформаций играют:

· интенсивность деформаций сдвига

;

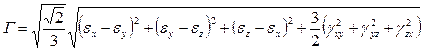· интенсивность деформаций

;

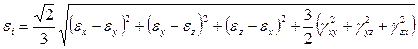· октаэдрические деформации

.

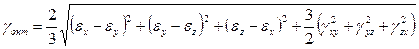Тензор скоростей деформаций

,

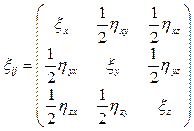где 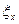, , 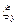, , 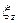, 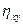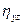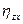- линейные и угловые скорости деформаций, которые вычисляются через скорости 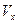, , 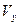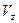по формулам

, ,

, ,

, .

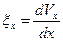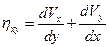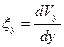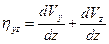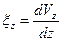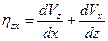При развитых пластических деформациях

.

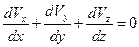Интенсивность скоростей деформаций сдвига

.

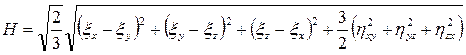Главные оси скоростей деформаций, главные скорости линейных деформаций определяются аналогично, как для тензора деформаций.

В технологических расчетах логарифмические деформации подсчитываются по формулам:

, , ,

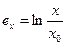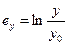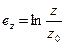гд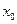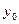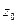е , , и - начальные и текущие размеры тела в направлении главных осей.

Задачи

6.1 Определить линейные и угловые деформации согласно рис. 8.

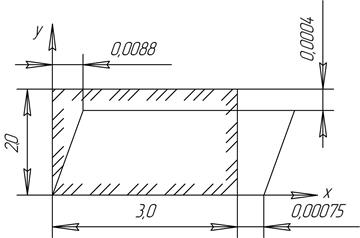
Рис. 8

6.2 Какая запись верно отражает запись тензора деформаций:

, ,

,

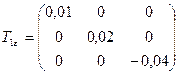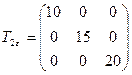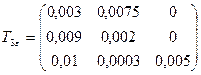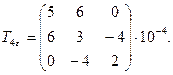
6.3 В точке тела имеются следующие компоненты деформаций: 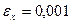, , 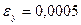, , 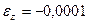, 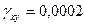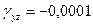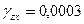. Вычислить глав­ные деформации и их ориентировку по отношению к осям , , .

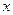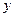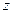6.4 Деформированное состояние тела описывается следующим тензором:

.

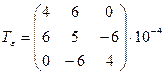Найти три взаимно перпендикулярных направления, которые остаются таковыми и после деформации.

6.5 При малой деформации тела каждая точка испытывает смещения (в 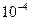мм), задан­ные следующими уравнениями:

,

,

.

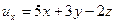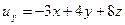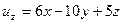Записать тензор деформаций и составить уравнение для определения главных деформа­ций.

6.6 При малой деформации кубика с ребром 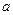каждая его точка испытывает смеще­ния, заданные следующими уравнениями:

,

,

.

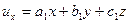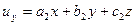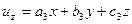Найти относительное изменение объема кубика и его линейные размеры после деформа­ции.

6.7 Известен тензор деформаций

.

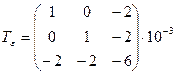Определить направления, в которых происходит лишь растяжение или сжатие.

6.8 Привести к диагональному виду следующие тензоры деформации:

, .

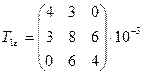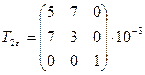6.9 Для плоского деформированного состояния ( 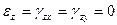) вывести фор­мулы для определения главных деформаций.

6.10 Деформированное состояние задано в виде следующего тензора:

.

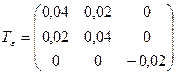Определить:

а) главные деформации;

б) девиатор деформаций и второй инвариант девиатора деформаций в главных осях;

в) конечные размеры деформируемого тела, если начальные размеры со­ста­вили 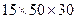мм.

6.11 Плита длиной 1200 мм, шириной 360 мм и толщиной 5 мм растягивается равно­мерно при растяжении в продольном направлении до тех пор, пока ее длина не увеличится до 1440 мм без изменения ширины. Найти:

а) конечные главные деформации;

б) конечные размеры плиты.

Решение.Выбрав следующие направления осей: длина 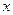, ширина 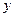, тол­щина 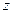, по­лучаем

, ;

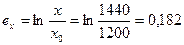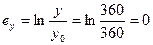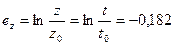, так как .

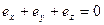Из уравнения

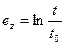
получае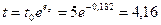м

мм.

Следовательно, размеры плиты после деформации будут следующими: длина 1440 мм, ширина 360 мм и толщина 4,16 мм.

6.12 Конечный диаметр прутка равен 40 мм, а длина 2400 мм. Этот пруток был подверг­нут равномерной пластической деформации растяжением от начального диаметра 60 мм. Определить:

а) первоначальные размеры прутка;

б) конечные деформации.

6.13 В процессе деформации первоначально квадратная сетка линий искази­лась так, что расстояние между деформированными квадратами в долевом на­правлении увеличи­лось в 4 раза по сравнению с первоначальным расстоянием. Найти:

а) конечные деформации, если процесс деформации является линей­ным растяже­нием;

б) конечные деформации, если ширина детали остается постоянной.

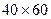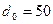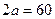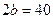6.14 На стальной лист была нанесена сетка со стороной квадрата 50 мм после деформа­ции она стала прямоугольной с размерами мм. Определить вели­чину конеч­ных деформаций. Изменится ли результат задачи, если рассматривать круглую сетку с мм, которая превратилась бы в эллипс с главными осями мм и мм?

6.15 Полоса длиной 250 мм была растянута до 300 мм. Считая напряженное со­стояние линейным, материал изотропным, а объем неизменным, найти дефор­мации по ширине и толщине полосы.

6.16 Пруток из изотропного материала был растянут таким образом, что его длина уве­личилась в 1,2 раза. Каким стал конечный диаметр прутка, если началь­ный диаметр 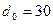мм? Каковы величины деформаций?

6.17 Плита длиной 2000 мм, шириной 400 мм и толщиной 10 мм деформирова­лась до тех пор, пока ее длина не стала равна 2800мм. Считая деформацию пло­ской, определить:

а) конечные деформации;

б) конечные размеры плиты;

в) интенсивность деформации.

6.18 Лист толщиной 6 мм, длиной 400 мм и шириной 300 мм растягивается до по­луче­ния продольной деформации 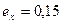. Считая толщину неизменной, опреде­лить конеч­ные размеры листа и интенсивность деформаций.

6.19 Труба с наружным диаметром 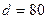мм, толщиной стенки 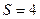мм и дли­ной 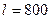мм подвергалась растяжению до 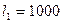мм. Считая материал изотроп­ным, найти компоненты деформации и ее интенсивность, а также конеч­ные размеры трубы.

6.20 Тензор скоростей деформации в декартовой ортогональной системе коорди­нат запи­сан следующим образом:

.

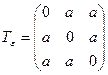Найти его главные значения и главные оси.

6.21 Заданы перемещения:

а) , , ;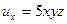

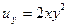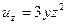б) , , .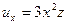

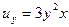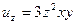Записать тензор деформации и проверить, удовлетворяются ли условия совмес­тимости.

6.22 Деформированное состояние в точке тела задано тензором бесконечно ма­лых де­формаций

.

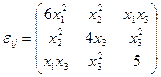Определить, удовлетворяются ли уравнения совместности.

6.23 Показатель деформированного состояния

.

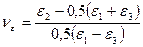Используя условие постоянства объема при пластических деформациях, записать его че­рез две деформации, а также через их отношения.

6.24 Считая деформацию пластической, рассмотреть значение показателя вида деформированного состояния для следующих слу­чаев:

а) чистый сдвиг, когда ;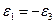

б) объемная схема деформаций, когда .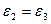

6.25 Используя условие постоянства объема, записать второй инвариант девиа­тора де­формаций через две деформации.

6.26 Даны значения 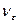: 0; +1; –1. Показать возможные случаи деформирован­ных состоя­ний, соответствующих указанным величинам.

6.27 На рис. 9 приведена схема изменения координатной сетки при волочении круг­лого сплошного профиля через коническую волоку. Дать анализ изменения линейных и угловых деформаций.

Рис. 9

6.28 Поле скоростей перемещений точек деформированного тела определяется уравнениями

,

,

.

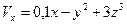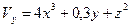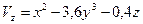Удовлетворяет ли это поле скоростей условию несжимаемости материала?

6.29 Круг диаметром 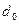, нанесенный в плоскости симметрии деформированного тела, в результате монотонного процесса деформирования превратился в эллипс, главные диаметры которого 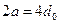, 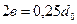. Определить величины главных конечных деформаций и интенсивность деформаций сдвига.

6.30 Деформированное состояние в точке тела задано тензором деформаций

.

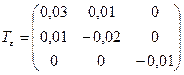Определить величины главных деформаций.

Решение. По виду тензора деформаций определяем, что компонента 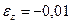является главной, так как 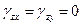. Величины двух других компонент находятся из уравнения:

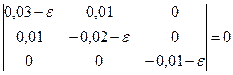
или

.

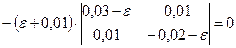Раскрывая определитель, получаем

;

;

.

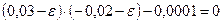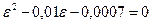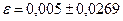Отсюда

; ; .

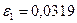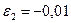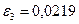6.31 Деформированное состояние в исследуемой точке тела, нагруженного внешними силами, характеризуется тензором малых деформаций, компоненты которого определены в декартовой системе координат:

.

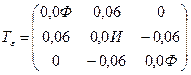Определить: 1) величины главных деформаций; 2) направления главных осей деформаций; 3) величины главных сдвиговых деформаций; 4) интенсивность деформаций; 5) вид деформированного состояния; 6) шаровой тензор деформаций в главных осях; 7) девиатор деформаций. Здесь Ф – число букв в фамилии; И – число букв в имени студента.