ГЛАВНЫЕ НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ. ОКТАЭДРИЧИСКИЕ НАПРЯЖЕНИЯ.
Задачи
1.1 Даны два симметричных тензора второго ранга:
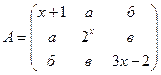 ,
, 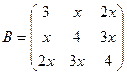 .
.
При каком значении 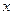 тензоры A и B равны между собой? Чему при этом равны а, б, в?
тензоры A и B равны между собой? Чему при этом равны а, б, в?
1.2 Записать в развернутой форме статические уравнения равновесия сил
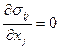 .
.
Решение. Индекс 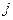 - немой, принимает все возможные значения 1,2,3 и по нему проводим суммирование. Если выбрано и зафиксировано определенное направление, то индекс
- немой, принимает все возможные значения 1,2,3 и по нему проводим суммирование. Если выбрано и зафиксировано определенное направление, то индекс 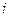 не меняется. Например, если выбрано направление
не меняется. Например, если выбрано направление 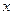 , то везде
, то везде 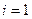 . В декартовой системе координат
. В декартовой системе координат 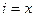 , в то время как
, в то время как 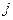 пробегает значения
пробегает значения 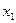 ,
, 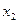 ,
, 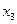 . Приняв последовательно
. Приняв последовательно 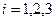 , получим уравнения равновесия сил для всех направлений:
, получим уравнения равновесия сил для всех направлений:
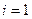 :
: 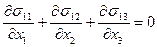 ,
,
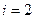 :
: 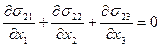 ,
,
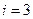 :
: 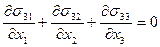 ,
,
или в декартовых координатах:
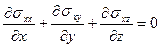 ,
,
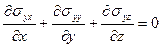 ,
,
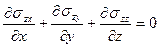 .
.
1.3 В трехмерном пространстве расшифровать уравнение
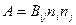 .
.
Решение. В одночлене два немых индекса 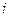 и
и 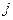 . Следовательно проводится двойное суммирование:
. Следовательно проводится двойное суммирование:
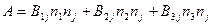 ,
,
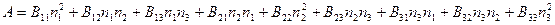 .
.
В начале провели суммирование по индексу 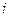 (
( 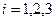 ), затем по индексу
), затем по индексу 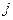 (
( 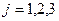 ).
).
1.4 Записать в развернутой форме следующие тензорные символы:
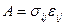 ,
, 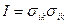 ,
, 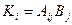 ,
, 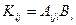 .
.
1.5 Найти значения выражений, содержащих символ Кронекера:
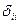 ,
, 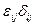 ,
, 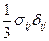 ,
, 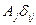 ,
, 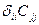 ,
, 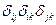 .
.
1.6 Записать в развернутом виде:
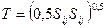 ,
, 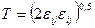 .
.
1.7 Известно, что составляющие полного напряжения на наклонной площадке в прямоугольной системе координат 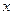 ,
, 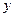 ,
, 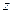 записываются следующим образом (уравнения Коши):
записываются следующим образом (уравнения Коши):
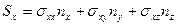 ,
,
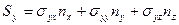 ,
,
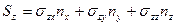 .
.
Записать их в тензорном обозначении.
Решение. Из последнего равенства видно, что индекс " 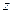 " относится к
" относится к 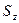 и стоит первым в обозначении напряжений. Предположим, что мы обозначили его через "
и стоит первым в обозначении напряжений. Предположим, что мы обозначили его через " 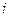 ". Второй индекс входит в выражение напряжений и направляющих косинусов. Обозначим его "
". Второй индекс входит в выражение напряжений и направляющих косинусов. Обозначим его " 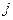 ". Следовательно, в тензорном обозначении указанные уравнения можно представить так:
". Следовательно, в тензорном обозначении указанные уравнения можно представить так:
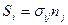 .
.
Таким образом, при 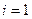 ,
, 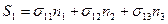 .
.
1.8 Нормальное напряжение на наклонной площадке записывается в виде
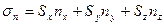
или
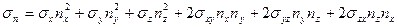 .
.
Дать тензорную запись этих уравнений, приняв 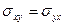 ,
, 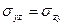 ,
, 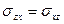 .
.
1.9 Первый и второй инварианты тензора напряжений имеют вид
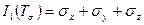 ,
,
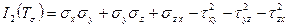 .
.
Представить их в тензорном обозначении.
1.10 Представить следующие формулы в тензорном обозначении:
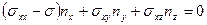 ,
,
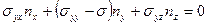 ,
,
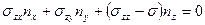 .
.
1.11 Определить ранг тензорных величин
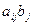 ,
, 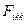 ,
, 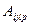 ,
, 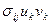 .
.
1.12 В системе координат 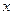 ,
, 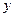 ,
, 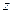 задан вектор
задан вектор 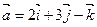 . Определить его компоненты в новой системе координат
. Определить его компоненты в новой системе координат 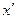 ,
, 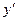 ,
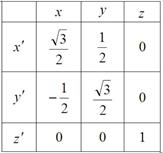
, 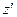 , направление осей которой задано табл.1 направляющих косинусов:
, направление осей которой задано табл.1 направляющих косинусов:
Таблица 1
Решение. На основании формулы (1) имеем:
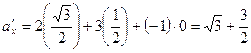 ,
,
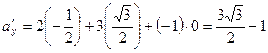 ,
,
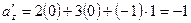 .
.
В системе координат 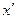 ,
, 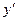 ,
, 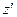 вектор записывается следующим образом:
вектор записывается следующим образом:
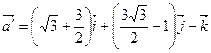 .
.
1.13 В системе координат 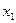 ,
, 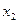 ,
, 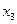 задан вектор
задан вектор 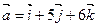 . Определить компоненты в новой системе координат
. Определить компоненты в новой системе координат 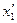 ,
, 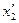 ,
, 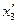 , полученной поворотом вокруг оси
, полученной поворотом вокруг оси 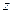 на угол
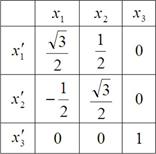
на угол 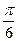 . Табл.2 направляющих косинусов имеет вид:
. Табл.2 направляющих косинусов имеет вид:
Таблица 2
1.14 Для тензора второго ранга
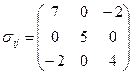 .
.
Определить компоненты 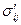 в системе координат
в системе координат 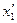 ,
, 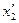 ,
, 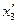 , заданной табл.3 направляющих косинусов.
, заданной табл.3 направляющих косинусов.
Таблица 3
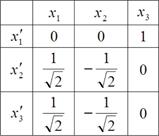
Решение. По формуле (2):
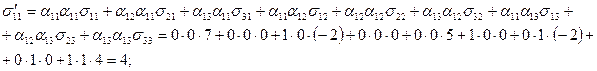
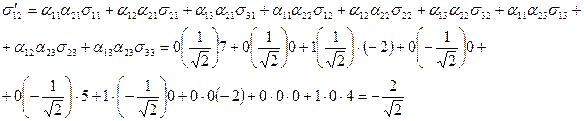
и т.д.
В результате
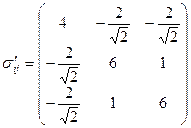 .
.
1.15 В системе координат 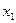 ,
, 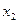 ,
, 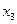 задан симметричный тензор второго ранга:
задан симметричный тензор второго ранга:
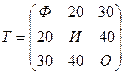 ,
,
где по главной диагонали Ф – число букв в фамилии, И – число букв в имени, О – число букв в отчестве студента.
Определить его компоненты в новой системе координат 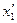 ,
, 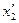 ,
, 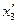 , полученной поворотом вокруг оси
, полученной поворотом вокруг оси 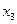 на угол
на угол 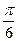 , направление осей которой задано табл.2 направляющих косинусов в задаче 1.13.
, направление осей которой задано табл.2 направляющих косинусов в задаче 1.13.
2. НАПРЯЖЕННОЕ СОСТОЯНИЕ В ОКРЕСТНОСТИ ЗАДАННОЙ ТОЧКИ
Напряженное состояние в точке деформируемого твердого тела характеризуется шестью числами и может быть описано симметричным тензором второго ранга – тензором напряжений.
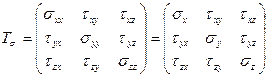 ,
,
где 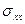 ,
, 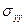 ,
, 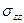 – нормальные напряжения,
– нормальные напряжения, 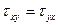 ,
, 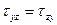 ,
, 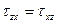 – касательные напряжения. Первый индекс соответствует координатной оси, перпендикулярной к площадке, на которой действует данное напряжение, а второй – оси, вдоль которой оно направлено. Поскольку у нормальных напряжений оба индекса одинаковы, то для них применяют и одномерную индексацию:
– касательные напряжения. Первый индекс соответствует координатной оси, перпендикулярной к площадке, на которой действует данное напряжение, а второй – оси, вдоль которой оно направлено. Поскольку у нормальных напряжений оба индекса одинаковы, то для них применяют и одномерную индексацию: 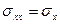 ,
, 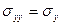 ,
, 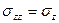 .
.
Если внешняя нормаль к площадке совпадает по направлению с положительным направлением соответствующей оси, то напряжение считается положительным, если оно направлено вдоль положительного направления оси, вдоль которой оно действует.
Полное напряжение на произвольной наклонной площадке:
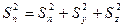 ,
,
где 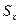 ,
, 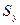 ,
, 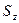 – проекции полного вектора напряжений на оси
– проекции полного вектора напряжений на оси 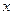 ,
, 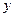 ,
, 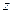 соответственно.
соответственно.
Нормальное напряжение на произвольной наклонной площадке:
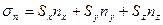 ,
,
где 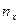 ,
, 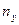 ,
, 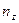 – направляющие косинусы, определяющие ориентацию площадки в пространстве.
– направляющие косинусы, определяющие ориентацию площадки в пространстве.
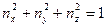 .
.
Полное касательное напряжение на произвольной наклонной площадке находится по правилу параллелограмма:
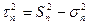 .
.
Уравнения, связывающие проекции на оси координат вектора полного напряжения, и напряжения, действующие на трех взаимно перпендикулярных площадках:
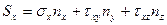 ,
,
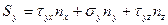 ,
,
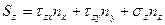 .
.
Компоненты напряжений связаны между собой дифференциальными уравнениями равновесия, которые в декартовой системе координат имеют вид:
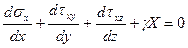 ;
;
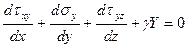 ;
;
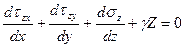 ;
;
где X, Y, Z – проекции объемных сил на оси координат; 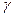 - плотность металла.
- плотность металла.
Задачи
2.1 Цилиндрический образец диаметром 10 мм подвергнут равномерному растяжению силой 10 кН. Определить напряжения, действующие внутри образца.
2.2 Напряженное состояние в точке задано следующими составляющими, кг/мм2:
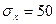 ,
, 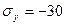 ,
, 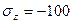 ,
, 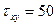 ,
, 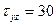 ,
, 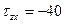 .
.
Записать тензор напряжений в системе СИ.
2.3 На рис. 2 показаны напряжения в декартовой и цилиндрической системах координат. Провести индексацию напряжений и записать их в форме тензора напряжений.
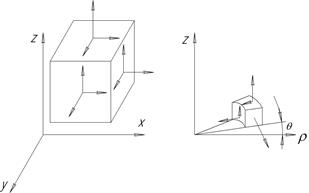
Рис. 2
2.4 На рис. 3 показаны различные случаи напряженного состояния в телах. Провести обозначение компонент напряжений, записать их в форме тензора напряжений, указать возможные нагружения тел внешними силами.
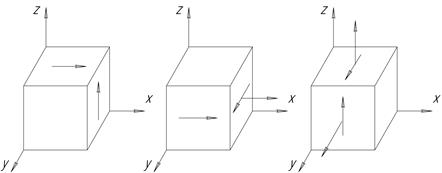
Рис. 3
2.5 Найти ошибки в записи тензора напряжений:
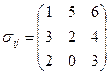 ,
, 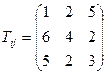 ,
, 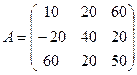 .
.
2.6 Напряженное состояние в некоторой точке тела задано тензором напряжений:
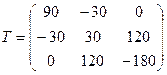 .
.
Размерность компонент тензора приведена в МПа. Для площадки, нормаль к которой определяется направляющими косинусами 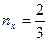 ,
, 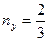 , найти полное
, найти полное 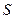 , нормальное
, нормальное 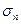 и касательное
и касательное 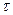 напряжения.
напряжения.
Решение.Известно, что 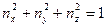 , откуда
, откуда
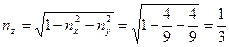 .
.
Тогда по формулам Коши:
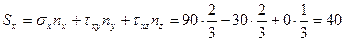 МПа,
МПа,
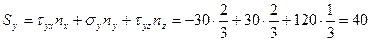 МПа,
МПа,
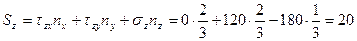 МПа.
МПа.
Полное напряжение:
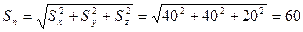 МПа.
МПа.
Нормальное напряжение:
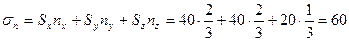 МПа.
МПа.
Касательное напряжение:
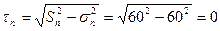 .
.
2.7 Напряженное состояние в некоторой точке тела задано тензором напряжений:
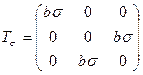 .
.
Определить значения полного, нормального и касательного напряжений на площадке с направляющими косинусами 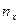 ,
, 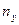 ,
, 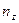 .
.
2.8 Напряженное состояние в точке тела задано в виде тензора:
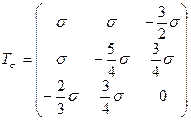 .
.
Определить значения полного, нормального и касательного напряжения на площадках, если:
а) 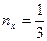 ,
, 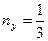 ;
;
б) 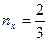 ,
, 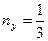 .
.
Сделать вывод по задаче.
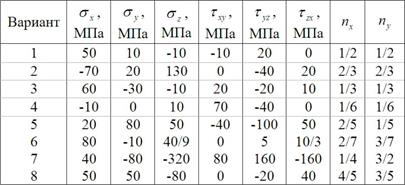
2.9 Определить значения полного, нормального и касательного напряжений по данным табл. 4.
Таблица 4
2.10 В точке тела на его границе (направляющие косинусы 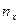 ,
, 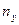 ,
, 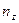 заданы) известны компоненты внешнего нагружения
заданы) известны компоненты внешнего нагружения 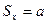 ,
, 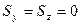 . Кроме того, известно, что возле заданной точки внутри тела
. Кроме того, известно, что возле заданной точки внутри тела 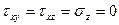 .
.
Вычислить остальные компоненты напряжений.
2.11 Напряженное состояние в точке тела задано тензором:
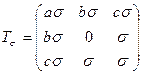 ,
,
где 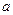 ,
, 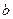 ,
, 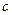 – константы.
– константы.
Определить их значения из условий, когда на площадке с направляющими косинусами 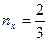 ,
, 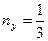 ,
, 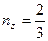 вектор полного напряжения
вектор полного напряжения 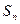 равен нулю.
равен нулю.
2.12 Напряженное состояние в точке тела задано тензором:
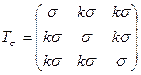 .
.
Определить значение 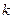 из условия, при котором на равнонаклонной площадке нормальное напряжение
из условия, при котором на равнонаклонной площадке нормальное напряжение 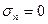 .
.
2.13 В задаче 2.12 изменить условия для определения 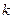 , считая, что полное напряжение
, считая, что полное напряжение 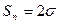 , а
, а 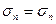 .
.
2.14 В задаче 2.12 изменить условия для определения 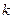 , считая, что нормальное напряжение
, считая, что нормальное напряжение 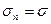 .
.
2.15 Построить эпюры нормальных и касательных напряжений в сечениях, наклонных к оси цилиндрического тела, с шагом 15º, подвергаемого растяжению силой Q 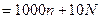 (кН), где
(кН), где 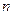 – номер группы (табл.5),
– номер группы (табл.5), 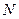 – номер студента в списке по алфавиту в составе группы. Дать их анализ.
– номер студента в списке по алфавиту в составе группы. Дать их анализ.
Таблица 5
2.16 Составить уравнение равновесия всех сил, действующих на выделенный элемент (рис. 4), в радиальном направлении.
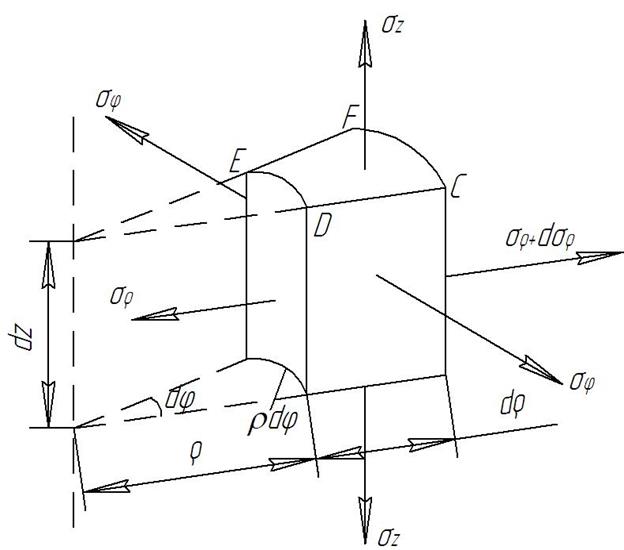
Рис. 4
2.17 Задано напряженное состояние в точке тела:
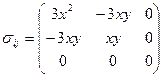 .
.
Определить, удовлетворяются ли условия равновесия?
2.18 Рассчитать компоненты массовых сил 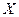 ,
, 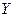 ,
, 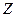 , если в любой точке сплошной среды выполняются уравнения равновесия, когда тензор напряжений задан в виде:
, если в любой точке сплошной среды выполняются уравнения равновесия, когда тензор напряжений задан в виде:
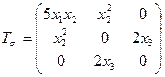 .
.
2.19 Записать тензор напряжений для тонкостенной трубы, подвергаемой
одновременному растяжению и кручению.
ГЛАВНЫЕ НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ. ОКТАЭДРИЧИСКИЕ НАПРЯЖЕНИЯ.
Главные нормальные напряжения выделяют из условия равенства определителя нулю
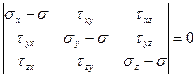 .
.
Отсюда
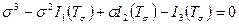 , (3)
, (3)
где 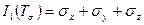 ,
,
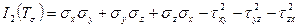 ,
,
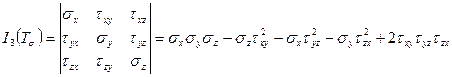 .
.
Решая кубичное уравнение (3), получаем три главных нормальных напряжения 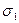 ,
, 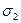 и
и 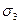 , которые располагаются следующим образом:
, которые располагаются следующим образом:
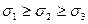 .
.
Коэффициенты 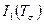 ,
, 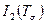 ,
, 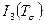 называются инвариантами тензора напряжений и их значения не зависят от выбранной системы координат.
называются инвариантами тензора напряжений и их значения не зависят от выбранной системы координат.
При решении методом Кардано подстановкой
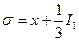
кубичное уравнение (1) приводится к виду
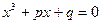 , (4)
, (4)
где 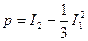 ,
, 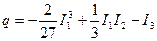 .
.
Если дискриминант приведенного уравнения (4) отрицателен, то все корни вещественные
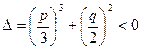 ,
,
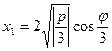 ,
, 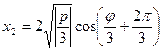 ,
, 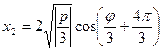 ,
,
где 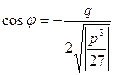 .
.
Если кубичное уравнение можно разложить на линейное и квадратное уравнения, то задача определения главных нормальных напряжений упрощается:
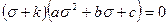 ;
;
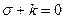 ,
, 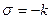 ;
;
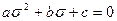 ,
, 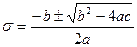 .
.
Каждому главному нормальному напряжению будет соответствовать главная ось, для которой направляющие косинусы находятся их решения системы уравнений:
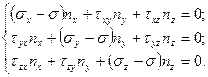 (5)
(5)
Сюда добавляется условие:
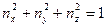 . (6)
. (6)
Для определения положения главных осей в два из трех уравнений системы (5) подставляются значения главных напряжений ( 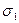 ,
, 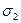 ,
, 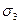 ), а в качестве третьего используется (6).
), а в качестве третьего используется (6).
Максимальные касательные напряжения подсчитываются по формулам
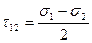 ,
, 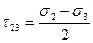 ,
, 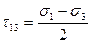 .
.
При 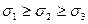 наибольшим из них будет
наибольшим из них будет 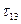 .
.
Октаэдрической является площадка, которая равно наклонена к главным направлениям напряжений. Октаэдрическое нормальное напряжение
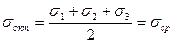 ,
,
а октаэдрическое касательное напряжение в главных осях
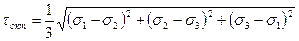
или в произвольных осях
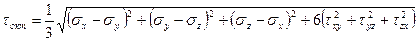 .
.
Задачи
3.1 Записать тензор напряжений через его главные значения для следующих случаев:
а) линейное напряженное состояние;
б) плоское напряженное состояние (рассмотреть возможные случаи);
в) объемное напряженное состояние (рассмотреть возможные случаи).
3.2 Напряженное состояние в точке тела задано одним из следующих тензоров:
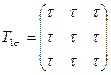 ,
, 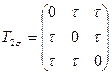 ,
, 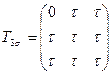 ,
,
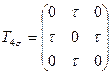 ,
, 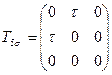 ,
, 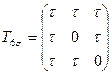 .
.
Определить главные нормальные напряжения и направления главных осей. Затем в тензорах изменить "+" на "-" и сделать вывод.
Решение.
 .
.
Для определения главных нормальных напряжений через заданные значения компонент напряжений в произвольной системе координат составим определитель
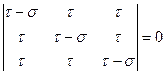 .
.
Раскроем его по первой строке
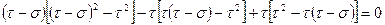 .
.
Получим кубическое уравнение в виде произведения линейного и квадратного уравнений
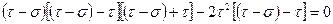 .
.
Тогда
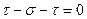 ,
, 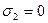 ,
,
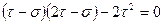 ,
,
отсюда 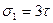 ,
, 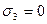 .
.
Таким образом, наблюдается случай линейного растяжения. При подстановке 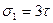 получаем следующую систему для определения
получаем следующую систему для определения 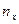 ,
, 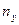 ,
, 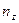 , описывающих положение главной оси 1 в пространстве:
, описывающих положение главной оси 1 в пространстве:
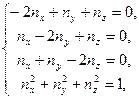
откуда 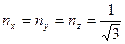 .
.
Для  уравнения сводятся к виду
уравнения сводятся к виду
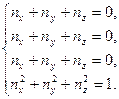
Их недостаточно для однозначного определения второй и третьей главных осей. Следовательно, любая пара взаимно перпендикулярных осей, перпендикулярных направлению 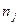 от
от 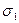 , может служить главными осями. Это очевидно из понятия линейного растяжения.
, может служить главными осями. Это очевидно из понятия линейного растяжения.
3.3 Найти главные значения напряжений и направления главных осей тензора напряжений
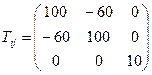 (МПа).
(МПа).
Решение. Составим определитель и раскроем по третьей строке:
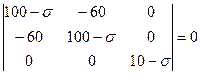 .
.
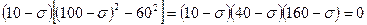 .
.
Отсюда 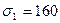 МПа,
МПа, 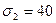 МПа,
МПа, 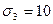 МПа.
МПа.
Определим направление главных осей.
Для 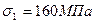 ,
,
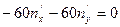 ,
,
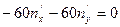 ,
,
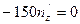 .
.
Решая эту систему, получаем 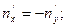
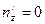 .
.
Из условия 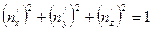 найдем
найдем 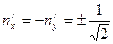 .
.
Для 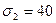 МПа,
МПа,
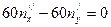 ,
,
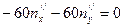 ,
,
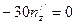 .
.
Решая эту систему, получаем 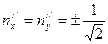 ,
, 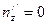 .
.
Для 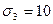 МПа,
МПа,
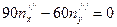 ,
,
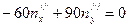 .
.
Тогда 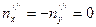 ,
, 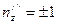 .
.
3.4 Напряженное состояние в точке, отнесенное к системе декартовых координат, записано в виде тензора.
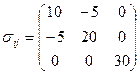 .
.
Величина составляющих тензора дана в 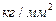 . Нужно вычислить величину и направление главных напряжений.
. Нужно вычислить величину и направление главных напряжений.
Решение. Одну составляющую главных напряжений можно определить сразу же из данного тензора, а именно 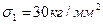 . Нормальные составляющие напряжения можно получить из первых двух уравнений, когда
. Нормальные составляющие напряжения можно получить из первых двух уравнений, когда 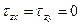 .
.
Тогда, определяя коэффициенты направляющих косинусов и задавая определитель равным нулю, получим
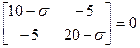 ,
,
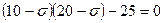 ,
,
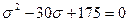 ,
,
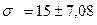 .
.
Отсюда
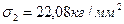 ,
,
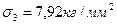
Направляющие косинусы можно определить из записи тензора напряжений. В данной задаче видно, что
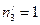 ,
, 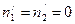 ,
,
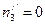 ,
, 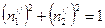
и
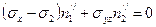 .
.
Возведя в квадрат последнее уравнение и определив одновременно направляющие косинусы, получим
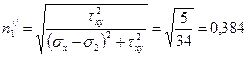 ,
, 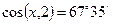 ,
,
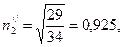
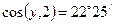 .
.
Таким же образом находим
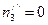 ,
,
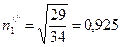 ,
, 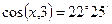 ,
,
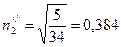 ,
, 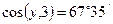 .
.
3.5 На рис. 5 показаны три взаимно перпендикулярные плоскости, проходящие через рассматриваемую точку, с действующими на них напряжениями. Вычислить главные напряжения.
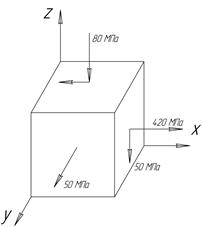
Рис. 5
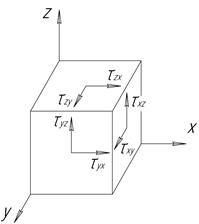
Рис. 6
3.6 Для заданного напряженного состояния (рис. 6), представляющего собой положение трех чистых сдвигов во взаимно перпендикулярных плоскостях, определить главные нормальные напряжения и максимальные касательные напряжения, если 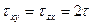 и
и 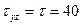 МПа.
МПа.
Решение.Для определения главных нормальных напряжений можно воспользоваться кубическим уравнением (3). После подстановки компонент напряжений получаем следующее кубическое уравнение:
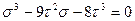 ,
,
где 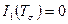 ,
, 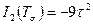 ,
, 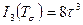 .
.
По условию 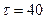 МПа, тогда
МПа, тогда
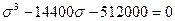 .
.
Левую часть последнего уравнения можно разложить на множители:
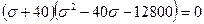 .
.
Приравнивая к нулю первый сомножитель, находим один из корней уравнения 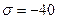 МПа.
МПа.
Решив квадратное уравнение
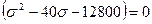 ,
,
найдем остальные два корня: 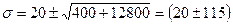 МПа или
МПа или 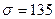 МПа,
МПа, 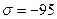 МПа.
МПа.
С учетом правила индексов для главных напряжений 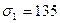 МПа,
МПа, 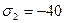 МПа,
МПа, 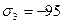 МПа.
МПа.
Максимальное касательное напряжение
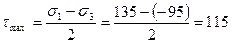 МПа.
МПа.
3.7 На рис. 7 приведены различные напряженные состояния в главных осях. Дать обозначения главных нормальных напряжений; указать вид напряженного состояния; показать площадки, на которых действуют максимальные касательные напряжения, обозначить их.
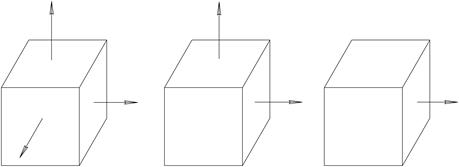
Рис. 7
3.8 Напряженное состояние в точке тела задано одним из следующих тензоров:
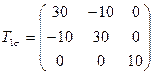 ,
, 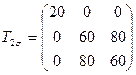 ,
,
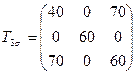 ,
, 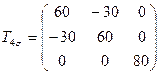 .
.
Определить главные напряжения и направления главных осей.
3.9 Для плоского напряженного состояния ( 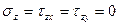 ) вывести формулы для определения главных нормальных напряжений. Для этого случая записать также формулы максимальных касательных напряжений.
) вывести формулы для определения главных нормальных напряжений. Для этого случая записать также формулы максимальных касательных напряжений.
3.10 Вычислить величины максимальных и октаэдрических касательных напряжений, если напряженное состояние задано одним из следующих тензоров:
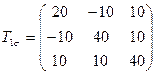 ,
, 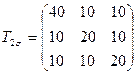 ,
, 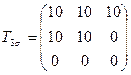 .
.
3.11 Найти выражения для расчета линейного, квадратного и кубического инвариантов тензора напряжений в главных осях для следующих случаев:
а) линейное напряженное состояние;
б) плоское напряженное состояние;
в) объемное напряженное состояние.
3.12 Вычислить главные значения и инварианты симметричного тензора напряжений
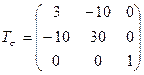 .
.
3.13 Главные нормальные напряжения в данной точке тела приведены в табл. 6:
Таблица 6
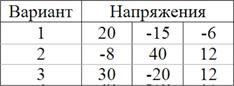
Присвоить численным значениям обозначения 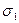 ,
, 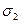 ,
, 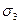 и вычислить максимальные касательные напряжения
и вычислить максимальные касательные напряжения 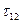 ,
, 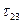 ,
, 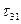 .
.
3.14 Доказать, что 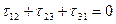 .
.
3.15 Определить главные напряжения и направления главных площадок, если напряженное состояние в точке задано следующими компонентами: 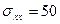 МПа,
МПа, 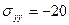 МПа,
МПа, 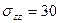 МПа,
МПа, 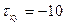 МПа,
МПа, 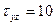 МПа,
МПа, 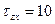 МПа.
МПа.
Решение.
1) Определяем инварианты заданного напряженного состояния:
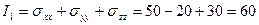 МПа;
МПа;
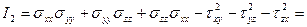
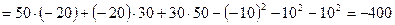 МПа;
МПа;
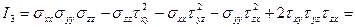
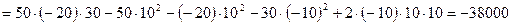 МПа.
МПа.
2) Определяем коэффициенты уравнения (4):
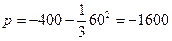 ,
, 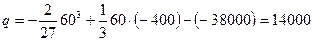 .
.
Определим дискриминант приведенного уравнения:
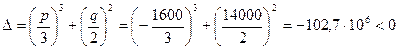 .
.
Так как дискриминант отрицателен, значит все корни приведенного уравнения вещественные.
3) Вычисление величин главных напряжений. Для решения проведенного уравнения применим формулу Кардано:
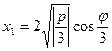 ,
, 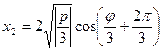 ,
, 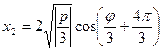 ,
,
где 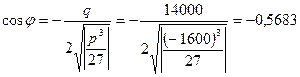
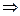
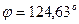 ;
;
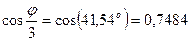 ;
; 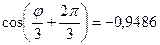 ;
; 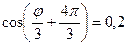 ;
;
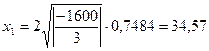 ,
, 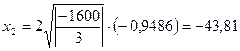 ,
, 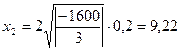 .
.
Окончательно получим:
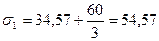 МПа,
МПа,
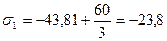 МПа,
МПа,
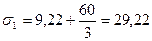 МПа.
МПа.
Проверка правильности вычисления главных напряжений: так как 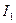 ,
, 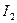 и
и 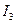 – инварианты, значит их значения постоянны. Ранее были получены их значения в заданной системе координат. Сейчас же найдем их значения в главной системе координат:
– инварианты, значит их значения постоянны. Ранее были получены их значения в заданной системе координат. Сейчас же найдем их значения в главной системе координат:
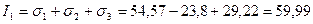 МПа;
МПа;
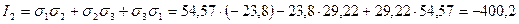 МПа;
МПа;
 МПа.
МПа.
Результаты вычислений 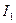 ,
, 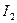 и
и 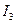 в рамках допустимых отклонений совпадают с результатами, полученными в п. 1 решения.
в рамках допустимых отклонений совпадают с результатами, полученными в п. 1 решения.
4) Определяем направляющие косинусы главных площадок. Система уравнений для определения 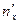 ,
, 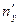 ,
, 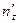 имеет следующий вид:
имеет следующий вид:
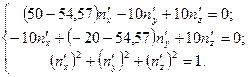
Решение этой системы: 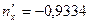 ,
, 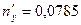 ,
, 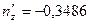 . Условия проверки выполняются:
. Условия проверки выполняются: 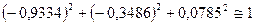 .
.
Система уравнений для определения 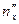 ,
, 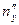 ,
, 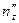 имеет следующий вид:
имеет следующий вид:
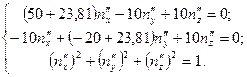
Решение этой системы: 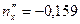 ,
, 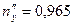 ,
, 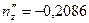 . Условия проверки выполняются:
. Условия проверки выполняются: 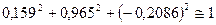 .
.
Система уравнений для определения 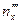 ,
, 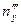 ,
, 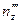 имеет следующий вид:
имеет следующий вид:
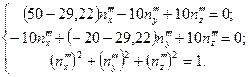
Решение этой системы: 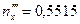 ,
, 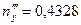 ,
, 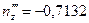 . Условия проверки выполняются:
. Условия проверки выполняются: 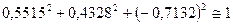 .
.
3.16 Определить главные напряжения методом Кордано и направления главных напряжений, если напряженное состояние в точке нагруженного тела задано тензором напряжений.
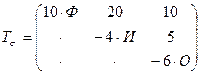 ,
,
где по главной диагонали Ф – число букв в фамилии, И – число букв в имени, О – число букв в отчестве студента.
3.17 Пластинка под действием главных нормальных напряжений 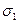 и
и 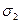 растягивается по двум взаимно-перпендикулярным направлениям. Определить нормальное и касательное напряжение на площадке с нормалью
растягивается по двум взаимно-перпендикулярным направлениям. Определить нормальное и касательное напряжение на площадке с нормалью 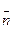 .
.
3.18 Тонкая пластинка равномерно растягивается по двум взаимно перпендикулярным направлениям. Определить нормальные и касательные напряжения на любой площадке с нормалью 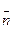 , приняв
, приняв 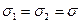 .
.
3.19 Тонкая пластинка в одном направлении сжимается, в другом растягивается, причем 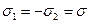 . Определить нормальные и касательные напряжения на площадках, наклонных к сторонам пластинки под углом
. Определить нормальные и касательные напряжения на площадках, наклонных к сторонам пластинки под углом 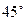 .
.
3.20 В точке тела имеется следующая система напряжений 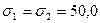 МПа,
МПа, 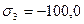 МПа. Определить нормальное, касательное и полное напряжения на октаэдрических площадках, проведенную через данную точку.
МПа. Определить нормальное, касательное и полное напряжения на октаэдрических площадках, проведенную через данную точку.
Дата добавления: 2016-07-27; просмотров: 3930;











