ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
Основной закон упругости может быть записан в следующей форме:
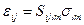 ,
,
где 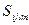 – упругие константы.
– упругие константы.
Применяется и следующий вид этого уравнения:
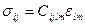 .
.
В случае ортотропного тела закон Гука через технические константы выражается таким образом:
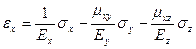 ,
, 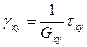 ;
;
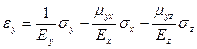 ,
, 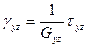 ;
;
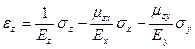 ,
, 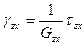 .
.
Часто вместо индексов 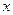 ,
, 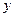 ,
, 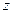 принимают индексы 1, 2, 3. Например,
принимают индексы 1, 2, 3. Например, 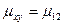 .
.
Ввиду изотропного материала основной закон упругости в прямой форме выражается формулами
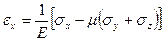 ,
, 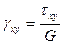 ;
;
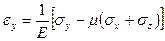 ,
, 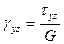 ;
;
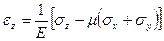 ,
, 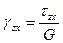 .
.
Его можно представить также и в виде двух законов: закона изменения объема
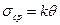
и закона упругого изменения формы тела 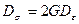 .
.
Здесь 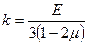 – объемный модуль упругости.
– объемный модуль упругости.
Закон Гука в обратной форме
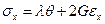 ,
, 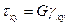 ,
,
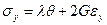 ,
, 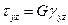 ,
,
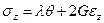 ,
, 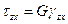 ,
,
где 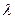 - коэффициент Ляме,
- коэффициент Ляме,
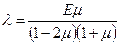 .
.
Модуль сдвига
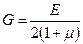 .
.
Задачи
7.1 Определить относительные линейные, угловые и объемные деформации в изотропном теле по данным табл. 7:
Таблица 7
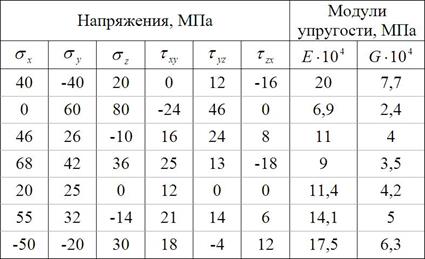
7.2 Из уравнения, выражающего обобщенный закон упругости для изотропного материала, получить выражение закона Гука для следующих случаев:
а) одноосное растяжение;
б) одноосное сжатие;
в) двухосное растяжение;
г) 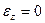 .
.
7.3 Для неметаллических ортотропных материалов определены упругие постоянные в табл. 8.
Таблица 8
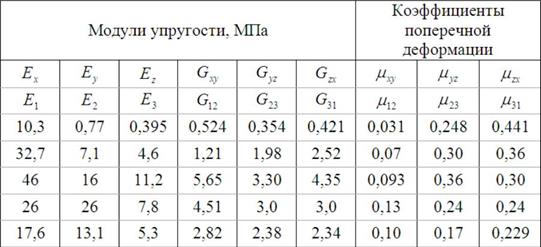
Для напряженного состояния, заданного тензором
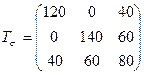 ,
,
определить линейные, угловые и объемные деформации.
7.4 Компоненты материального тензора, входящего в уравнения упругости 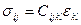 , при изотропном теле можно представить следующим образом:
, при изотропном теле можно представить следующим образом:
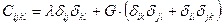 .
.
Для данного случая записать закон Гука через постоянные 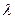 и
и 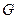 .
.
7.5 Показать, что 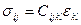 можно разбить на две группы:
можно разбить на две группы:
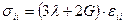 и
и 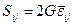 .
.
Здесь 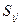 и
и 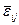 – компоненты девиаторов напряжений и деформаций.
– компоненты девиаторов напряжений и деформаций.
7.6 Замерены следующие деформации табл. 9:
Таблица 9
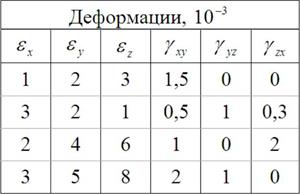
Используя данные по упругим постоянным, приведенным в задачах 7.1 и 7.2, определить напряженные состояния материала. Используя данные таблицы, представить закон Гука в виде законов изменения объема и формы тела. Показать также зависимости 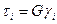 .
.
7.7 Стержень длиной 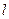 равномерно растянут в пределах упругой деформации на величину
равномерно растянут в пределах упругой деформации на величину 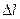 . Определить перемещения точек тела
. Определить перемещения точек тела 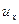 ,
, 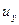 ,
, 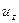 и возникающие напряжения для следующих случаев:
и возникающие напряжения для следующих случаев:
а) стержень имеет круглое сечение;
б) стержень имеет квадратное сечение.
7.8 Определить, под действием каких сил находится круглый цилиндрический стержень, если его перемещения выражаются функциями
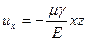 ,
, 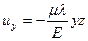 ,
, 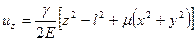 .
.
7.9 Вывести следующие зависимости между упругими постоянными:
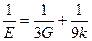 ,
, 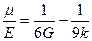 .
.
7.10 Образец упруго растянут с относительной деформацией 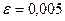 . Модуль нормальной упругости 196 ГПа, коэффициент Пуассона
. Модуль нормальной упругости 196 ГПа, коэффициент Пуассона 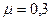 . Определить относительное изменение объема образца
. Определить относительное изменение объема образца 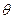 .
.
7.11 Куб размерами 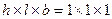 м подвергнут осадке на величину
м подвергнут осадке на величину 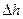 в пределах упругости. Коэффициент Пуассона
в пределах упругости. Коэффициент Пуассона 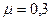 . Определить объемную деформацию.
. Определить объемную деформацию.
7.12 Стальная деталь нагружена и замерены следующие упругие деформации: 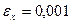 ,
, 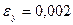 ,
, 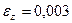 ,
, 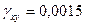 ,
, 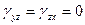 . Найти напряженное состояние детали, если
. Найти напряженное состояние детали, если 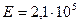 МПа,
МПа, 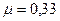 .
.
Дата добавления: 2016-07-27; просмотров: 2829;











