ПЛОСКИЕ И ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ

Для решения плоских задач теории упругости часто используется функция напря­жений Эри 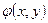. Компоненты напряжений представляются частными произ­водными

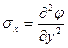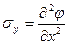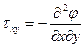, , . (7)

При этом уравнения равновесия удовлетворяются тождественно, а условие со­вместности превращается в бигармоническое уравнение

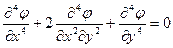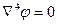или . (8)

В случае решения задачи в полярных координатах компоненты напряжений и ус­ловие со­вместности можно представить в виде выражений

, , ,

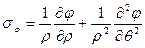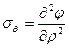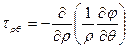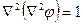
или

.

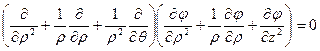Если напряжения распределены симметрично относительно оси, то 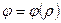имеет вид

,

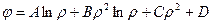где 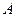, , 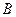, 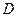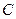– постоянные, определяемые из заданных условий на контуре.

Исходя из этого, можно найти напряжения в толстостенных цилиндрах с ра­диу­сам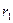и и 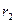при наличии внутреннего 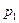и внешнего 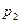давлений:

.

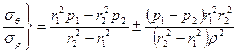Для плоского напряженного состояния

, , ,

, , .

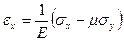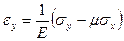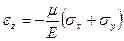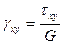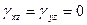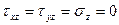Для плоской деформации

, ,

, ,

, .

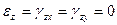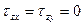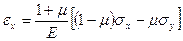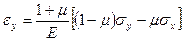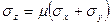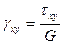Задачи

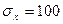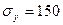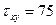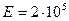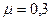8.1 Даны величины напряжений МПа, МПа, МПа. Опре­де­лить деформации, если деталь изготовлена из стали МПа, . Определить изменение объема.

8.2 В плите из алюминиевого сплав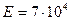а ( МПа, 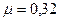) при ее деформа­ции толщина остается неизменной, а деформации составят 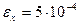, , 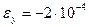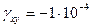. Определить возникающие напряжения.

8.3 Найти связь между константам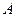и и 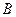, при которой функция 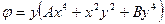будет функцией Эри. Определить компоненты напряжений.

8.4 Проверить, могут ли при осесимметричной деформации тела функциями на­пряже­ний служить

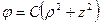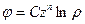, (n=0, 1, 2, 3),

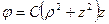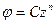, (n=1, 2, 3),

где C – постоянная.

8.5 Доказать, что функция напряжения Эри 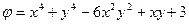удовлетво­ряет бигармоническому уравнению 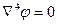. Найти компоненты напряже­ния, считая дефор­мацию плоской. Записать уравнения для определения деформаций.

8.6 Кольцо единичной толщины окручивается двумя парами сил, приложен­ных соот­ветственно к внутренней и наружной боковым поверхностям. Убедиться в том, что в каж­дой точке

, .

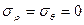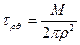8.7 Стальной цилиндр, внешний диаметр которого 300 мм и толщина стенки 60 мм, подвергнут внутреннему давлению 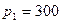МПа. Определить величину наи­больших растя­гивающих, сжимающих и касательных напряжений. Построить эпюры 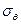, 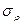и .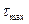

8.8 В задаче 8.5 поменять условие, т.е. считать, что действует не внутреннее, а внеш­нее давление. Определить те же величины.

8.9 Принять, что стальной цилиндр (задача 8.7) подвергнут не только внутрен­нему 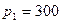МПа, но и внешнему давлению 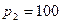МПа. Определить те же вели­чины.

8.10 Определить напряжение в стальном контейнере, состоящем из втулки ( 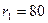мм, 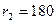мм) и корпуса ( 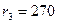мм). Натяг по диаметру при посадке втулки 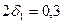мм, а внутреннее давление 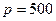МПа. Построить эпюры напряже­ний.

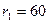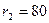8.11 Дана система, состоящая из корпуса и двух втулок с размерами: мм, мм, 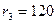мм и 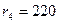мм. Натяг между первой и второй втул­ками 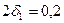мм, а между втулкой и корпусом 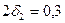мм. Внутреннее давление 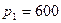МПа. Корпус и втулка стальные. Определить напряжения и построить их эпюры.

8.12 Дана прямоугольная пластина шириной 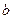, длиной 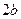(рис. 10), по кром­кам кото­рой действуют внешние силы, равномерно распределенные по ее тол­щине, равной еди­нице. Под действием этих сил в пластине возникает напряжен­ное состояние, описываемое функцией напряжений в виде полинома четвертой степени

.

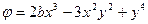Требуется:

1) Проверить возможность существования такой функции напряжений.

2) По функции напряжений найти выражения компонентов напряжений.

3) Выяснить характер распределенных по кромкам пластины внешних сил, под действием которых имеет место данная система напряжений, и постро­ить эпюры напря­жений.

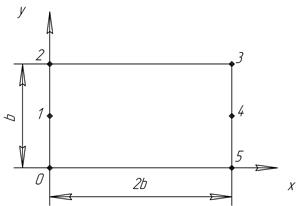
Рис. 10

Решение.

1) Для выполнения проверки существования заданной функции напряже­ний вы­полним ее дифференцирование:

; ; ; ;

; ; ; ;

; ; .

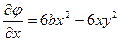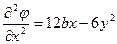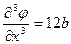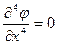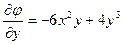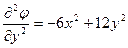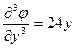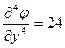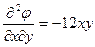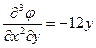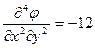Подставив четвертые производные в бигармоническое уравнение (8), ви­дим, что оно удовлетворяется: 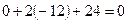. Следовательно, напряженное состояние пла­стины, выраженное заданной функцией напряжений, возможно.

2) Компоненты напряжений, действующих по кромкам пластины, равны:

; ; .

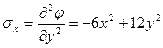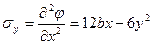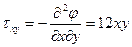3) Используя функциональные компоненты напряжений в пластине, по­строим соответствующие эпюры напряжений по контуру пластины на каждой ее боковой стороне.

Сторона 0-1-2 ( 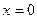, 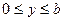). На этой грани действуют напряжения , :

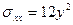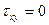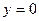(точка 0) , ;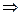

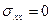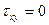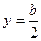(точка 1) , ;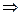

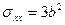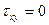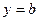(точка 2) , .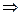

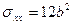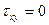Сторона 2-3 ( 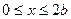, 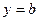). На этой грани действуют напряжения , :

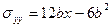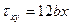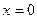(точка 2) , ;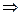

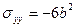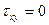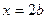(точка 3) , .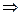

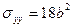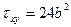Сторона 3-4-5 ( 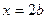, 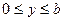). На этой грани действуют напряжения , :

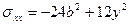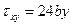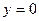(точка 5) , ;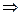

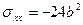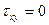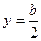(точка 4) , ;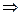

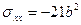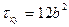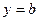(точка 3) , .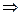

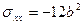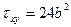Сторона 0-5 ( 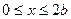, 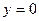). На этой грани действуют напряжения , :

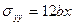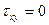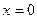(точка 0) , ;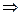

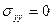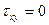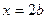(точка 5) , .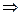

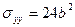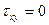По полученным результатам строим эпюры 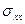, 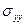и 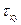, которые приве­дены на рис. 11.

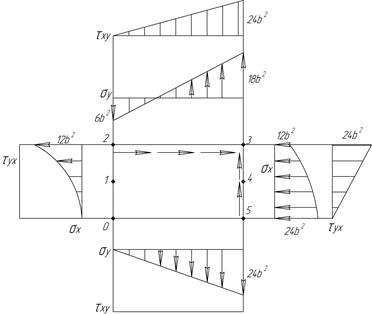
Рис. 11

8.13 Дана прямоугольная невесомая пластина (рис. 10), по кромкам которой дей­ст­вуют внешние силы, равномерно распределенные по ее толщине, равной единице.

Требуется:

1) Проверить возможность существования функции напряжений в виде поли­нома четвертой степени

,

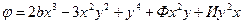с помощью бигармонического уравнения. Здесь Ф – число букв в фамилии, И – число букв в имени студента.

2) По функции напряжений найти выражения компонентов напряжений.

3) Выяснить характер распределения по кромкам пластины внешних сил путем построения эпюры напряжений по контуру пластины на каждой ее боко­вой стороне, ис­пользуя рассчитанные данные в точках 0, 1, 2, 3, 4, 5.

4) Записать тензор напряжений и тензор деформаций для центральной точки пластины, приняв 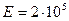МПа, , .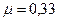

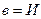8.14 Толстостенная достаточно длинная труба из однородного материала нахо­дится одно­временно под действием равномерного внутреннего и наружного дав­лений в упругом состоянии. Определить напряженно-деформированное состояние трубы.

Решение.Используем цилиндрическую систему координат. Направим ко­ординат­ные линии 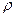, , 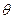, 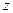соответственно по радиусу трубы, в окружном направ­лении и вдоль оси трубы (рис. 12).

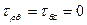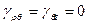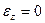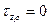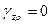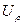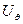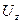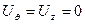Так как напряженно-деформированное состояние трубы является осесим­метрич­ным, то , . Так как труба достаточно длинная, то можно принять схему плоского деформированного состояния, т.е. . Тогда , . Из трех компонент вектора перемещения , , две , а 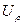зависит только от координаты 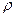, т.е. материальные точки трубы перемещаются в радиальных направле­ниях.

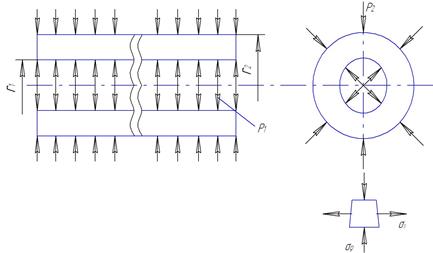
Рис. 12

Система уравнений, описывающих напряженно-деформированное состоя­ние тол­стостенной трубы, состоит из одного уравнения статического равновесия

,

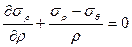соотношений между деформациями и перемещениями

, ,

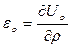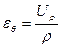физических уравнений, связывающих напряжения с деформациями:

,

,

,

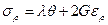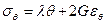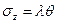где 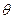– объемная относительная деформация ( ).

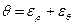Таким образом, имеем пять уравнений с пятью независимыми перемен­ными 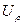, , 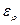, , 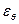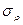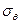. Поставленная задача статически определима.

Решим задачу в перемещениях. Подставим в физические уравнения вместо дефор­маций перемещения по формулам

,

.

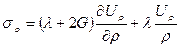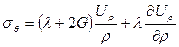Полученные выражения напряжений подставим в уравнения равновесия. получим дифференциальное уравнение Ляме в перемещениях:

,

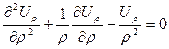решение которого имеет вид

.

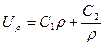Тогда

,

,

,

.

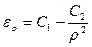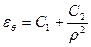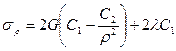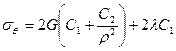Постоянные 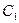и 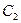найдем из граничных условий: на внутренней поверхно­сти трубы ( 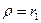) 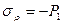, на наружной поверхности ( 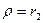) 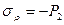. Подставим эти значе­ния в третью формулу:

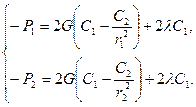
Решая эту систему двух уравнений относительно 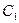и 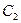, найдем

,

.

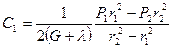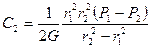Подставим эти выражения, получим окончательно

,

.

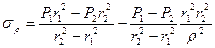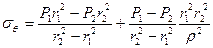Зная 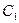и 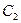, можно найти и перемещение 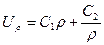и осевое напряже­ние 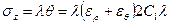, которое постоянно во всех точках трубы.

Теперь рассмотрим три случая.

1) Труба нагружена внутренним давлением. В этом случае .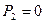

,

.

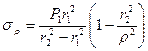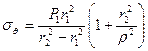На рис. 13, а показаны эпюры распределения радиального и окружного на­пряжений по толщине стенки трубы при нагружении внутренним давлением.

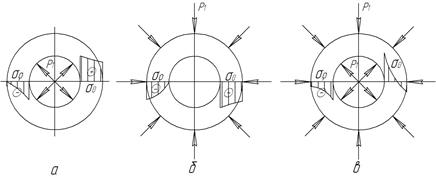
Рис. 13

Окружное напряжение является растягивающим, а радиальное – сжимаю­щим. У внутренней поверхности 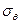достигает наибольшего значения

,

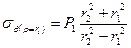радиальное напряжение при этом равно .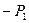

2) Труба нагружена только наружным давлением. В этом случае .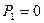

,

.

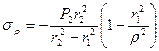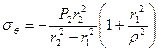Эпюры напряжений по толщине стенки трубы для этого случая нагружения пред­ставлены на рис. 13, б. Окружное и радиальное напряжения – сжимающие напряжения.

3) Труба нагружена одновременно наружным и внутренним давлением. Соотно­шение между внутренним и наружным давлениями полагаем таким, что внутрен­ний и наружный радиусы трубы увеличиваются. Эпюры напряжений по толщине стенки трубы для этого случая нагружения представлены на рис. 13, в. Окружные напряжения около внутренней поверхности – растягивающие, а около наружной поверхности – сжи­мающие.

8.15 Определить напряженное состояние контейнера при прессовании. Контей­нер со­стоит из двух цилиндрических втулок, посаженных друг на друга с натягом.

Исходные данные:

а) внутренний радиус - 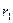(мм) – ;

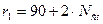б) наружный радиус - 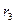(мм) – ;

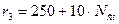в) радиус сопряжения втулок - 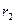(мм) – ;

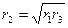г) внутреннее давление в контейнере при прессовании, 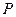(МПа) – ;

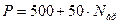д) натяг ;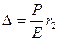

е) давление посадки ;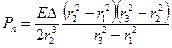

ж) допустимое напряжение материала втулок 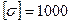МПа;

з) модуль упругости 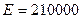МПа.

Этапы расчета:

1) Привести упругое решение задачи для толстостенной трубы, нагружен­ной внешним и внутренним давлением (задача 8.14).

2) Рассчитать напряженное состояние в контейнере от давления прессо­вания при 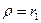, , 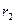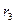. Построить эпюры напряжений.

3) Рассчитать напряженное состояние в контейнере во втулках контей­нера от давления посадки. Построить эпюры напряжений.

4) Используя метод суперпозиции сил, построить суммарные эпюры на­пряже­ний от давления прессования и давления посадки.

5) Проверить работоспособность втулок контейнера по III теории прочно­сти .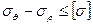

6) Показать во сколько раз увеличивается прочность составного контей­нера по сравнению с однослойным контейнером.