РАЗЛОЖЕНИЕ ТЕНЗОРА НАПРЯЖЕНИЙ
Тензор напряжений может быть разложен на два тензора – шаровой 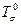 и девиатор
и девиатор 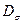 , т.е.
, т.е. 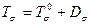 . Их компоненты связаны зависимостью
. Их компоненты связаны зависимостью
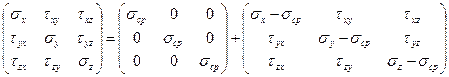 ,
,
где 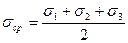 .
.
Главные значения девиатора напряжений определяются из решения кубического уравнения, полученного при раскрытии определителя:
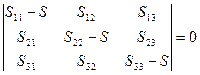 ,
,
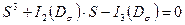 ,
,
где
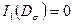 ;
;
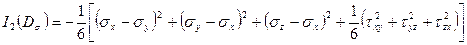 ;
;
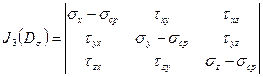 .
.
При изучении сплошного напряженного состояния важное значение имеет октаэдрическое касательное напряжение 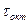 , интенсивность нормальных
, интенсивность нормальных 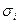 и касательных
и касательных 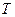 напряжений, которые определяются по выражениям в главных осях:
напряжений, которые определяются по выражениям в главных осях:
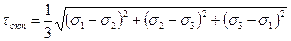 ,
,
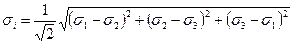 ,
,
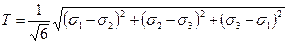 .
.
Задачи
4.1 Показать запись второго инварианта девиатора напряжений через его главные значения.
4.2 Определить величину первого инварианта девиатора напряжений 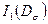 .
.
4.3 Разложить тензор напряжений для линейного напряженного состояния:
а) растяжение;
б) сжатие.
Дать схемы главных напряжений для тензора напряжений, шарового тензора и девиатора.
4.4 Записать тензор напряжений, когда тело в процессе деформирования испытывает только упругое изменение объема, а изменения формы не происходит.
4.5 Записать тензор напряжений, когда тело в процессе деформирования испытывает только изменение формы, а упругого изменения объема не происходит.
4.6 Объяснить, почему составляющая девиатора напряжений в направлении главной оси 1 будет положительной, а в направлении главной оси 3 – отрицательной.
4.7 Для некоторой точки тела известен тензор напряжений 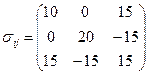 .
.
Разложить его на шаровой тензор и девиатор, посчитать инварианты тензора.
Решение. Найдем компоненты шарового тензора
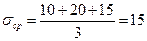 .
.
Определим компоненты девиатора
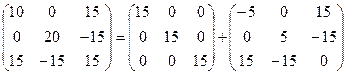 .
.
Инварианты тензора будут следующие:
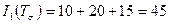 ;
;
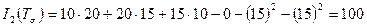 ;
;
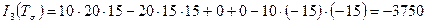 .
.
4.8 Разложить тензоры напряжений (МПа)
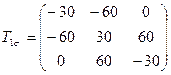 ,
, 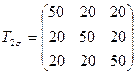 ,
,
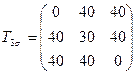 ,
, 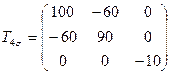
на шаровые и девиаторы; определить значения второго инварианта девиатора.
4.9 Два тела из одинакового материала испытывают однородное напряженное состояние. Известен тензор напряжений для однородного тела
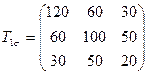 .
.
Составить тензор 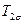 для второго тела, если известно, что относительное изменение объема обоих тел одинаково, а девиатор для второго тела
для второго тела, если известно, что относительное изменение объема обоих тел одинаково, а девиатор для второго тела
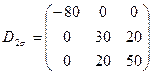 .
.
Определить также главные значения полученного тензора.
4.10 Для точки тела известны девиатор напряжений
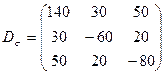
и одно из нормальных напряжений, например 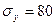 МПа. Определить тензор напряжений.
МПа. Определить тензор напряжений.
4.11 Для точки тела известен первый инвариант тензора напряжений 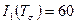 МПа и девиатор напряжений
МПа и девиатор напряжений
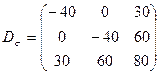 .
.
Определить главные значения девиатора напряжений, а через них и главные нормальные напряжения. Записать тензор напряжений.
4.12 Напряженные состояния записываются в виде тензоров:
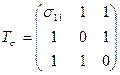 ,
, 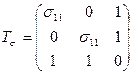 .
.
Разложить их на шаровые тензоры и девиаторы, определить их значение из условия равенства нулю одного из главных значений девиатора напряжений.
4.13 В теории пластичности широко используется показатель
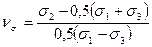 ,
,
где 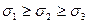 .
.
Рассмотреть его значения для следующих частных случаев:
а) линейное растяжение;
б) линейное сжатие;
в) двустороннее растяжение при 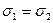 ;
;
г) двустороннее сжатие при 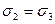 ;
;
д) чистый сдвиг, когда 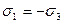 .
.
Достаточно ли этого показателя, чтобы полностью охарактеризовать напряженное состояние?
4.14 Показать различные варианты записи 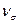 через отношения напряжений.
через отношения напряжений.
4.15 Главные компоненты тензора напряжений могут быть представлены следующим образом:
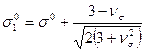 ,
, 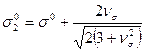 ,
, 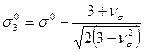 ,
,
где 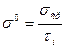 ,
, 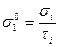 и т.д.
и т.д.
Какие значения принимают 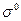 ,
, 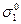 ,
, 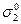 и
и 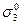 для случаев, указанных в задаче 4.12.
для случаев, указанных в задаче 4.12.
4.16 В каких случаях напряженное состояние может быть полностью охарактеризовано отношением двух напряжений 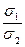 ?
?
Дата добавления: 2016-07-27; просмотров: 3125;











