Пластичность кристаллов. Описание

При растяжении кристаллические материалы ведут себя обычно так, как показано на кривых рис. 1.7. На рис. 1.7, а показана кривая растяжения железа, из которой видно, что при некотором значении напряжения проходит резкая граница начала пластической деформации и течение происходит без роста напряжений.

Соответствующее напряжении носит название предела текучести. На рис. 1.7,6 приведена (для меди) кривая напряжение — деформация, из которой видно, что переход к интервалу пластической деформации в этом случае не настолько резок, как для железа. После того как наступило течение, дальнейшая пластическая деформация монокристалла может быть двух основных типов: скольжением или двойникованием.

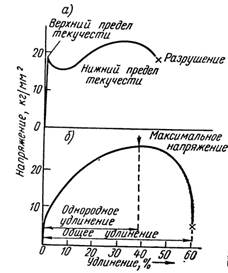
Рис. 1.7. Кривые напряжение — удлинение: а) для железа, б) для меди

При скольжении (рис. 1.8, а) верхняя половина кристалла перемещается относительно нижней вдоль определенной кристаллографической плоскости (плоскости скольжения) таким образом, что атомы перемещаются на целое число межатомных расстояний и в результате сохраняется непрерывность кристаллической решетки. Пересечение плоскостей скольжения с поверхностью образца дает обычно четко различимую линию скольжения.

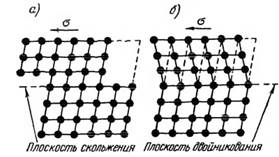
Рис. 1.8. Схемы: а) скольжения и б) двойникования в кристаллах

При двойниковании (рис. 1.8,6) перемещения большинства атомов происходят на расстояния, меньшие межатомных, и решетка в деформированной области является зеркальным изображением решетки в недеформированной области. Плоскость, разделяющая эти решетки, носит название плоскости двойникования.

Все процессы деформации металлов сводятся к осуществлению скольжения или двойникования. Напряженное состояние при этом может быть сложным, но для того чтобы происходила пластическая деформация, необходимо действие касательных напряжений. Для иллюстрации рассмотрим цилиндрический кристалл с площадью поперечного сечения А (рис. 1.9), подвергающийся растяжению некоторой силой Р.

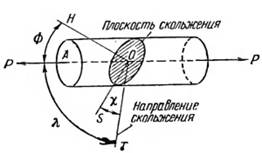
Рис. 1.9. Соотношение между плоскостью скольжения, направлением скольжения и осью растяжения в кристалле

При этом деформация скольжения происходит в плоскости скольжения, заштрихованной на рисунке; площадь этого сечения составляет А/cosФ, где Ф — угол между нормалью к плоскости скольжения ОН и осью растяжения. Приложенная сила Р распределяется вдоль этой плоскости и может быть разложена на силу, нормальную к плоскости скольжения, РcosФ и силу, действующую в плоскости скольжения в направлении OS и равную PsinФ.

Последняя сила называется силой сдвига. Таким образом, приложенное напряжение (отношение силы к площади сечения) может быть разложено на нормальное напряжение (P/А)cos²Ф, стремящееся оторвать атомы друг от друга, и касательное напряжение (P/A)cosФsinФ, стремящееся сдвинуть атомные плоскости друг относительно друга.

Как правило, скольжение идет в том направлении, где расстояния между атомами являются наименьшими. При этом необходимо знать критическое напряжение сдвига в плоскости скольжения и в направлении скольжения. Если направление скольжения соответствует ОТ на рисунке, то критическое напряжение сдвига дается соотношением

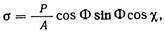
где λ — угол между направлениями О и ОТ. Обычно эту формулу употребляют в более простом виде

где λ — угол между направлением скольжения ОТ и осью растяжения.

Таким образом, критическое напряжение сдвига имеет наибольшую, величину, когда плоскость скольжения наклонена под углом 45° к оси растяжения и становится меньше для углов как больших, так и меньших 45° Когда плоскость скольжения становится почти перпендикулярной к оси растяжения (Ф<<45°), появляется тенденция к отрыву атомов друг от друга под действием приложенного напряжения, а не к скольжению. Когда плоскость скольжения почти параллельна оси растяжения (Ф>>45°), касательное напряжение также мало, но в этом случае из-за того, что велика площадь A/cosФ, на которой распределена нагрузка.

Итак, пластическая деформация происходит под действием касательных напряжений, и поэтому пластическое поведение материала в значительной степени зависит от вида механических испытаний. Например, очень пластичный материал может разрушиться без всяких проявлений пластичности, если его испытывать в состоянии трехосного или гидростатического растяжения, так как при этих условиях критическое напряжение сдвига в любой плоскости равно нулю. Точно так же материалы, которые в обычных условиях растяжения являются хрупкими, могут быть пластичными, если вести испытания при таких условиях, когда касательные напряжения велики, а нормальные малы.

Многочисленные эксперименты по деформации монокристаллов показывают, что скольжение подчиняется следующими закономерностям:
1) направление скольжения почти всегда совпадает с направлением плотной упаковки атомов,
2) плоскость скольжения обычно является плоскостью с наиболее плотной упаковкой атомов,
3) из набора плоскостей и направлений скольжения действующими являются те, для которых критическое напряжение сдвига является наибольшим.

Так, например, в кристаллах с гранецентрированной кубической структурой скольжение происходит в плоскостях {111} и направлениях <110>. В кристаллах с гексагональной плотноупакованной структурой скольжение происходит вдоль направлений <1120>, так как эти направления характеризуются наибольшей плотностью упаковки атомов. В то же время в кристаллах е гексагональной структурой активная плоскость скольжения зависит от осевого отношения с/а. Так, например, для таких металлов, как кадмий и цинк, осевое отношение составляет соответственно 1,886 и 1,856, плоскости с наибольшей плотностью атомов— это плоскости базиса {0001}, и скольжение идет по этим плоскостям.

Если осевое отношение заметно меньше величины 1,633, соответствующей плотнейшей упаковке атомов, то плотность упаковки атомов в плоскостях базиса уменьшается и одновременно уменьшается расстояние между этими плоскостями. Так, например, в цирконии (с/а= 1,589) и титане (с/а = 1,587) скольжение идет по плоскостям {1010} при комнатной температуре и {1011} при повышенных температурах. В металлах с объемноцентрированной кубической структурой имеется единственное плотноупакованное направление < 111 > и несколько семейств плоскостей с примерно эквивалентной плотностью упаковки атомов {112}, {110} и {123}. Выбор этих плоскостей зависит от природы металла и температуры испытания.

При пластической деформации обычно осуществляется закон критического напряжения сдвига, согласно которому скольжение происходит вдоль определенной плоскости скольжения и тогда, когда напряжение достигает критической величины. В большинстве кристаллов, обладающих высокой симметрией в расположении атомов, существует несколько кристаллографически эквивалентных плоскостей и направлений скольжения.

Например, в кристаллах с гексагональной плотноупакованной структурой имеются три системы скольжения, составленные из одной плоскости скольжения и трех направлений в этой плоскости. В то же время в кристаллах с объемноцентрированной кубической структурой число возможных систем скольжения значительно больше. В таких случаях скольжение сначала происходит в той плоскости и в том кристаллографическом направлении из возможных систем, где действуют максимальные касательные напряжения.

Все сказанное подтверждается, например, при испытании на растяжение кристаллов цинка. Этот металл имеет гексагональную плотноупакованную структуру, и поэтому в нем процесс скольжения может идти только в плоскости базиса, так что результирующая кривая напряжение— деформация, будет зависеть от наклона этой плоскости по отношению к оси растяжения.

Величина Ф зависит от ориентировки кристалла во время выращивания из расплава, и поэтому можно получить кристаллы с различными Ф. Соответствующие кривые напряжение — деформация дают различные значения напряжения течения. Но, вследствие существования закона критического напряжения сдвига, зависимости критического напряжения сдвига (напряжения, действующего в плоскости скольжения и в направлении скольжения) от деформации почти точно совпадают для всех образцов в пределах ошибки эксперимента.

Важность представления о критическом напряжении особенно очевидна на примере изгиба кристалла, плоскость базиса которого ориентирована перпендикулярно к оси растяжения, т. е. в случае, когда ф = 0. В противоположность хрупкому разрушению такого кристалла, происходящему при растяжении, мы можем наблюдать пластичное поведение, так как касательное напряжение в плоскости скольжения равно нулю только при испытаниях на растяжение.

С другой стороны, если взять кристалл с плоскостью базиса, ориентированной параллельно оси растяжения (т. е. Ф = 90°), такой кристалл будет хрупко разрушаться при любом виде механических испытаний. Для этого кристалла, несмотря на большую величину силы сдвига, действующая площадь плоскости скольжения А/cosФ настолько велика и, следовательно, критическое напряжение сдвига настолько мало, что его недостаточно для начала скольжения.

На поверхности деформированного кристалла наблюдают полосы скольжения, каждая из которых состоит из большого числа линий скольжения. Таким образом, деформация неоднородна; в одних кристаллографических плоскостях идет интенсивная деформация, в то время как в лежащих между ними плоскостях с теми же индексами деформация отсутствует. Процесс скольжения при этом напоминает сдвиг колоды карт.

Однако практически при механических испытаниях картина усложняется, так как концы образца, закрепленные в машине, не могут двигаться в стороны. При этом центральная часть образца изменяет ориентировку и происходит поворот как плоскости скольжения, так и направления скольжения по отношению к оси растяжения кристалла. (Это поведение можно продемонстрировать на стереографической проекции кристалла.)

Для удобства будем считать, что поворачивается не кристалл, а ось растяжения. На рис. 1.10, а приведена стереографическая проекция, иллюстрирующая кристаллографию деформации в гранецентрированных кубических кристаллах. Направление оси растяжения Р показано внутри стереографического треугольника. Углы между Р и направлениями (нормалями к плоскостям) [101] и [111] составляют соответственно λ, и Ф. Активная система скольжения соответствует плоскости (111) и направлению в ней [101]. По мере того как идет деформация, происходит изменение ориентировки кристалла и точка Р перемещается по штриховой кривой в сторону [101], т. е. угол λ уменьшается, а угол Ф возрастает.

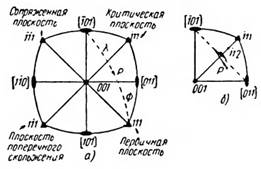
Рис. 1.10. Стереографические проекции, иллюстрирующие: а) системы скольжения в кристаллах с гранецентрированной кубической структурой, б) явление «перелета» при деформации скольжения

Когда скольжение происходит в одной системе (первичной системе скольжения), плоскость скольжения поворачивается из своего положения, отвечающего максимуму критического напряжения сдвига, до тех пор, пока ориентировка кристалла не достигнет линии на стереографической проекции, соединяющей точки [001] и [111]. После этого скольжение может происходить как в первичной, так и во вторичной системе скольжения (сопряженной системе) (111) [011], так как для этих систем равны компоненты касательного напряжения.

Следовательно, при одновременном скольжении в двух системах или сложном скольжении решетка будет поворачиваться таким образом, чтобы напряжения в двух системах скольжения оставались одинаковыми, и ось приложения нагрузки будет .перемещаться вдоль линии симметрии [001]—[111] по направлению к точке [112].

Эта простая схема деформации обычно наблюдается в чистых металлах, не подвергшихся специальным обработкам. При исследовании кристаллов сплавов, а также закаленных и облученных монокристаллов чистых металлов, обычно оказывается, что скольжение в- первичной системе продолжается и после того, как ориентировка кристалла достигнет линии симметрии.

При этом происходит так называемый «перелет» и кристалл продолжает поворачиваться в сторону [101], т. е. в направлении первичного скольжения. После того как эта добавочная деформация достигнет некоторой величины, происходит резкий переход ко вторичной системе скольжения, и кристалл начинает поворачиваться в противоположном направлении, опять заходя за линию симметрии.

Этот процесс, .схематически показанный на рис. 1.10, 6, связан с тем, что скольжение во вторичной системе должно идти с пересечением линий скольжения, оставшихся от скольжения в первичной системе. Такой процесс иногда более затруднен, чем появление новых полос скольжения в сравнительно недеформированной области даже при неблагоприятном напряженном состоянии. Ниже будет показано, что процесс пересечения труднее идет в металлах с низкой энергией дефектов упаковки, например, в а-латуни.

Анализ проведенных выше кривых напряжение — деформация показывает, что после конца процесса течения для дальнейшего продолжения деформации требуется непрерывное увеличение 'напряжения, т. е. напряжение течения деформированного металла увеличивается с ростом деформации. Сопротивление металла дальнейшему пластическому деформированию по мере увеличения деформации носит название деформационного упрочнения.

Степень деформационного упрочнения различна для металлов с различной кристаллической структурой; она невелика для металлов с гексагональной структурой, например цинка и кадмия, где скольжение идет обычно только в одной системе плоскостей.

Упрочнение кубических кристаллов идет обычно значительно быстрее, но и в этом случае, если ограничить скольжение одной системой, коэффициент упрочнения, определяемый как наклон кривой напряжение—деформация на участке, соответствующем пластической деформации, имеет небольшую величину. Таким образом, этот тип упрочнения так же, как и «перелет», может быть связан с процессом скольжения в пересекающихся плоскостях.