Что такое стереографическая проекция

При рассмотрении кристаллографии пластической деформации целесообразно ввести понятие о стереографической проекции, с помощью которой удобно представлять плоскости, направления и углы в кристалле. Предположим, что исследуемый кристалл расположен в центре сферы (рис. 1.5, а).

При этом плоскость, например, плоскость (111), может быть определена точкой Р — пересечением нормали к этой плоскости с поверхностью сферы. Такая проекция носит название сферической. На рис. 1.5,6 показано, что угол между плоскостями (001) и (111) может быть измерен в градусах дуги большого круга между полюсами Р и Р'.

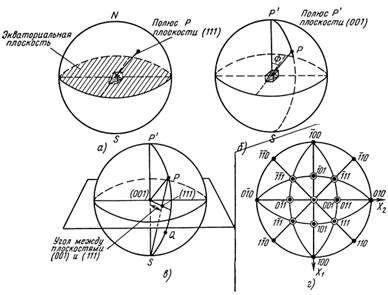
Рис. 1.5. Принципы построения стереографической проекции: а) плюс Р плоскости (111), б) угол между двумя полюсами Р и Р’ (в данном случае полюсов плоскостей (111) и (001), г) стереографическая проекция основных плоскостей в кубических кристаллах

Для того чтобы упростить проекцию и свести ее к плоскому изображению, применяют следующее построение. Соединяют прямыми полюсы плоскостей P, Р' и т. д. в верхней полусфере с «южным» полюсом сферы S (рис. 1.5,в). Пересечения этих прямых с горизонтальным экваториальным кругом дают стереографическую проекцию кристалла. Плоскости, дающие полюсы в нижней части сферы, например Q, могут быть спроектированы на стереографическую проекцию путем соединения с «северным» полюсом сферы.

На рис. 1.5 г приведена стереографическая проекция кристалла кубической системы, содержащая полюсы некоторых плоскостей семейств {100}, {110} и {111}. Кружками на проекции обозначены плоскости, проектируемые из южного полюса сферы, точками — плоскости, проектируемые из северного полюса сферы. Угол Ф между двумя плоскостями (двумя полюсами на сфере), как видно из рис. 1.5, в, равен углу, разделяющему эти точки при прохождении через них большого круга.

Часто для описания пластической деформации кристаллов высокой симметрии, например, относящихся к кубической системе, нет необходимости рассматривать всю стереографическую проекцию. В качестве иллюстрации рассмотрим кристаллы кубической системы. Легко убедиться, что кубическая элементарная ячейка имеет 3 четверных оси симметрии, 4 тройных оси и 6 двойных.

Четверные оси проходят через центр каждой грани куба параллельно ребру, тройные оси — через пространственные диагонали, двойные — через середины противоположных ребер или параллельных диагоналей граней. Анализ стереографической проекции, приведенной на рис. 1.5 г показывает, что плоскости симметрии делят проекцию на 24 эквивалентных стереографических треугольника, соответствующих 48 (24 в верхней и 24 в нижней полусферах) криволинейным треугольникам в сферической проекции.

Поэтому при анализе кристаллографии пластической деформации »кристаллов кубической системы часто ограничиваются рассмотрением треугольника, образованного полюсами (001), (011) и (111).

Важной особенностью стереографической проекции является то, что индексы любой плоскости одной зоны на стереографической проекции могут быть получены сложением индексов других плоскостей зоны, лежащих по обе стороны от этой плоскости. Например, плоскость (011) лежит на проекции между (001) и (010), плоскость (112) лежит между (111) и (001), плоскость (123) лежит между (112) и (011) и т. д.