Атомные модели дефектов. Нульмерные, или точечные дефекты

Дефекты, встречающиеся в кристаллах, чрезвычайно разнообразны, и мы ограничимся рассмотрением лишь тех типов дефектов, о которых с достаточной определенностью известно, что они влияют на пластические свойства кристаллов. Классификацию дефектов удобно проводить по геометрическому признаку и разделять дефекты на нульмерные, одномерные, двумерные и трехмерные.

Нульмерные, или точечные дефекты. Дефекты этого типа возникают, когда в кристаллических телах в малой области, размеры которой не превышают нескольких межатомных расстояний во всех трех измерениях, нарушается правильность кристаллической структуры. Дефекты такого типа могут возникать как при изменении химического состава кристаллов, так и при внешних воздействиях (например, пластической деформации или облучении).

В некоторых случаях обе эти причины могут вызывать появление одинаковых точечных дефектов.

Примесные дефекты. Дефекты химического происхождения, которые мы будем называть примесными дефектами, возникают, например, при образовании твердых растворов, когда введение атомов второго компонента не меняет типа кристаллической решетки растворителя. Рассмотрим на простейших примерах возникающие при этом дефекты кристаллической структуры.

В твердых растворах замещения точечные дефекты (в данном случае атомы растворенного элемента) замещают атомы растворителя в кристаллической решетке и распределяются статистически, неупорядоченно.

Схема расположения атомов в плоскости (100) материала с кубической структурой в этом случае показана на рис. 1.11, а и 1.11, б. Структуру такого типа имеют все твердые растворы элементов-металлов и химических соединений. В твердых растворах внедрения атомы растворенного элемента располагаются в промежутках между атомами растворителя, в основном сохраняющих свои положения в решетке.

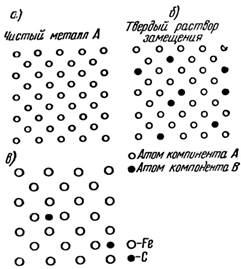
Рис. 1.11. Расположение атомов в кристаллической решетке твердых растворов: а) чистый металл А; б) твердый раствор замещения между металлами А и В; в) твердый раствор внедрения (плоскость (100) кристалла аустенита)

На рис. 1.11, в приведена схема расположения атомов при растворении углерода в у-железе (аустенит). Атом углерода при этом является внедренным атомом. Твердые растворы внедрения, как правило, возникают при растворении неметаллов с малым атомным радиусом (например, Н, С, N, В) в металлах переходных групп. Подробное рассмотрение структуры твердых растворов внедрения необходимо при обсуждении механизма деформации технических железоуглеродистых сплавов.

Возможно также образование твердого раствора вычитания, когда избыточные атомы растворенного элемента занимают нормальные положения в решетке, а некоторые места, предназначенные для атомов растворителя, остаются пустыми. Так, например, в кристалле вюстита — твердого раствора кислорода в закиси железа FeO — все узлы решетки, в которых должны находиться ионы кислорода, заполнены, а часть узлов, в которых должны расположиться ионы железа, вакантны.

В некоторых структурах, состоящих из двух компонентов, вакантными могут оказаться узлы обоих типов. Так, в структуре окисла титана ТіО, относящейся к структурному типу NaCl, могут быть незаполненные узлы, которые в идеальном кристалле должны быть заняты как ионами титана, так и ионами кислорода.

При рассмотрении точечных дефектов примесного .происхождения возможен приближенный расчет искажений, создаваемых атомом примеси в кристалле. В простейшем случае можно рассматривать упругий шар (атом примеси) в упругоизотропной матрице. Обозначим коэффициенты сжимаемости для атома примеси и матрицы соответственно н’ и н, коэффициенты Пуассона соответственно v' и v.

Атом примеси считаем шаром с начальным радиусом r_s', помещенным в сферическую полость матрицы с начальным радиусом r_s’. В результате взаимодействия упругой сферы и матрицы происходит деформация, и как сфера, так и полость в матрице приобретают .промежуточный радиус r_a.

При образовании твердых растворов замещения величины r_s' и r_s близки друг к другу, при образовании твердых растворов внедрения r_s' << r_s. В результате рассматриваемого процесса происходит искажение обеих сред, например, равномерное трехосное растяжение атома примеси, в матрице происходит сдвиг, пропорциональный r^-3 (r — расстояние от центра атома примеси), а также небольшое растяжение, пропорциональное концентрации атомов примесей.

Даже при небольшой атомной концентрации примесей с должно наблюдаться влияние примесей на общий удельный объем (плотность) материала, средний период решетки, измеряемый рентгеноструктурным методом, и упругие постоянные (модуль сдвига G и коэффициенты сжимаемости H). Эти соотношения могут быть записаны следующим образом:

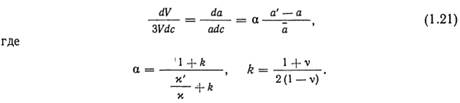
Из этих соотношений следует, что период кристаллической решетки при н’ = н должен линейно меняться с концентрацией атомов примесей (закон Вегарда). В действительности часто наблюдают отклонения от линейной зависимости между периодом решетки и концентрацией даже при малых концентрациях примесей.

Например, изменение периода решетки сплавов железо-ванадий, как видно из рис. 1.12, дает отклонение от линейной связи даже .при малых концентрациях ванадия. Данные, приведенные на рисунке, получены рентгеноструктурным методом с применением ионизационной регистрации интенсивности и точных гониометрических устройств.

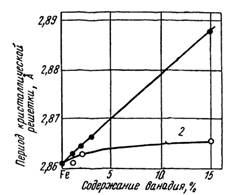
Рис. 1.12. Зависимость периода кристаллической решетки сплавов железо-ванадий от концентрации ванадия: 1 — теоретическая зависимость, 2 — опытная зависимость

Наконец, необходимо рассмотреть локальные искажения структуры, связанные с присутствием чужеродных атомов в кристаллической решетке. Степень искажения структуры определяется величиной среднеквадратичного статического смещения атомов из равновесных положении в решетке 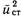которую можно определить по интенсивности дифрагированного рентгеновского излучения. Если представить атомы в виде упругих шаров, то можно показать, что

где с — концентрация твердого раствора, ΔR —разность атомных радиусов растворенного элемента и растворителя, γ — числовой множитель, учитывающий кристаллическую структуру материала. Для гранецентрированной кубической решетки γ = 7,8, для объемноцентрированной кубической решетки γ = 7,3.