Задачи-измерители. Описание и примеры

Роль и место задач в курсе физики выяснены и общепризнанным является их важное значение при проверке и оценивании знаний и умений учащихся. Решение задач как умение — цель обучения физике. Решение задач как процесс — способ выявления уровня успешности школьника в обучении, а сама задача — это измеритель того или иного качества знаний и умений.

Особенность задач заключается в том, что они являются многоцелевыми измерителями. Поэтому для проверки нужны задачи самых разнообразных типов, в частности, прямые и обратные задачи на расчет какой-то величины. Например.

Чему равно давление 4 кг кислорода, находящегося в баллоне объемом 2 м³ при температуре 29°С?

Чтобы решить эту задачу, учащиеся должны хорошо знать уравнение идеального газа по памяти. Преобразующая деятельность тут имеет математический характер:

Зная все компоненты этой формулы и запомнив единицы физических величин, учащиеся смогут (на основе умения производить действия с физическими величинами) найти искомую величину и правильно все это записать.

Таких расчетных задач учащиеся решают довольно много. Хорошо сказал о них П. А. Капица: «Обычно эти задачи сводятся к тому, что надо подставить заданные данные в нужные формулы, и тогда получить определенный ответ. Самостоятельность ученика проявляется только в том, чтобы правильно выбрать формулы, в которые нужно подставить данные».

В последнее время появилось много сборников задач, дидактических материалов и другой литературы, вмещающих задачи разнообразных типов и уровней сложности. Они требуют от учащихся самостоятельности мышления. Например.

Поплавок карбюратора массой 60 г и диаметром 3 см плавает в топливе поплавковой камеры. Учитывая действие сил поверхностного натяжения, определить силу Архимеда, действующую на поплавок.

Эта задача позволяет выяснить, умеют ли учащиеся оперировать знаниями, полученными в разных классах, и разобраться в комплексном проявлении различных физических закономерностей в одном техническом объекте — карбюраторе. Подобные задания полезны также при проверке уровня развитости политехнических представлений.

Иногда достаточно немного изменить условие задачи, взятой из сборников, и активизация мышления уже стимулирована. Приведем пример двух таких задач.

Два маленьких металлических шарика одинакового размера, имеющие заряд 5х10^-7Кл каждый, находятся на расстоянии в 30 см. С какой силой шарики отталкиваются друг от друга?

Маленький металлический шарик, имеющий электрический заряд 10^-6 Кл, приводится в соприкосновение с незаряженным шариком такого же размера, а затем шарики раздвигаются до расстояния 30 см. С какой силой шарики отталкиваются друг от друга?

Очень часто в литературе приводятся задачи, позволяющие измерить уровень овладения тем или иным методом решения. Например.

Стрела запущена с высоты 2 м от поверхности Земли вертикально вверх со скоростью 30 м/с. Найти положение стрелы относительно Земли через 4 с. (Ускорение свободного падения принять равным 10 м/с².)

Дождевые капли падают в безветренную погоду. Какова их траектория относительно Земли и относительно вагона, движущегося равномерно на прямолинейном участке пути? (Ответ поясните чертежом).

Подобные задачи не бесполезны для коллективного решения в классе, ибо знакомят с координатным методом, который дает возможность упростить изучение некоторых проблем. Однако использовать такие задачи в качестве измерителей нельзя. Это превышает требование программы и ведет к перегрузке учащихся. В то же время при углубленном изучении физики такие задачи могут быть объективными измерителями уровня овладения учащимся координатным методом.

Задачи как измерители помогают определить и много других образовательных качеств обучаемых, в частности, как развито теоретическое мышление. Например (IX класс). Найти математическое выражение зависимости плотности идеального газа от давления при постоянной температуре.

Решая ее, ученик должен вспомнить из курса VI класса, что с уменьшением объема данной массы газа соответственно увеличивается его плотность. Отсюда

По закону Бойля—Мариотта и следовательно .

Решение этой задачи позволяет определить умение ученика на основе теоретических знаний выявить существенные отношения между величинами, самостоятельно вывести новую (для него) физическую закономерность.

Теоретическое мышление предполагает ориентировку школьника на отыскание внутренних, существенных отношений, данных,, составляющих условие задачи. Это позволяет быстро и правильно решать однотипные задачи в обобщенном виде.

Если ученики не овладели обобщенным способом решения задач, если они к анализу условия задачи подходят не теоретически, а эмпирически (ориентируются прежде всего на внешние данные, на числовые значения величин), то при решении каждой новой задачи способ решения развертывают заново. В первом случае ученики, вооруженные теорией поиска, свободно решают все однотипные задачи, во втором — только отдельные.

Вот почему требование программы решать задачи в общем виде имеет большой дидактический смысл. Принцип построения проверочного задания в этом случае состоит в сочетании внутренней общности, однотипности задач с внешним различием их условий.

Не следует думать, что подбор измерителей на выявление сформированности теоретического мышления должен требовать от учащихся больших обобщений, систематизаций, классификаций и т. п. Так, сформированности действия анализа — это тоже признак развитости теоретического мышления, его основной компонент.

Смысл действия анализа заключается в том, что школьник, работая над условием задачи, выделяет в ней существенные отношения. Например, металлический шарик прикрепляют к пружине, второй конец которой держат в руке. Пружину растягивают и отпускают. Возникают гармонические колебания шарика. Возникнут ли колебания, если опыт повторить в состоянии невесомости?

При анализе задачи несущественным ученик посчитает то, что пружина закреплена рукой, а существенным — условия, при которых совершаются гармонические колебания в первом и во втором случаях. Поскольку в обоих случаях действие силы упругости остается, ученик на вопрос задачи отвечает положительно. Следовательно, диагностическое задание отвечает требованию валидности. Ученик сумел выделить в процессе анализа существенные отношения, от которых зависит успешное решение предложенной и подобных задач (условия, в которых может или не может проявляться данное явление).

Учащиеся VII класса обычно хорошо усваивают закон Ома, умеют его сформулировать, указать характер взаимосвязи между I и U, но часто не учитывают, что для того, чтобы рассчитать силу тока или напряжения, надо брать данные, относящиеся к одному и тому же участку цепи. Естественно, что при проверке знаний надо подобрать такой измеритель, который позволил бы выявить устранен этот пробел в их подготовке или нет.

Если это будет задача на закон Ома, в условии которой есть данные о простейшей цепи, то она не даст ответа об усвоении контролируемого качества. Если же в задаче будут данные, относящиеся к двум (нескольким) участкам цепи, то планируемая цель может быть достигнута. Например.

Два проводника с сопротивлением R₁=3 Ом и R₂=1 Ом соединены последовательно (рис. 7). Напряжение на концах проводника R₁ показывает вольтметр V₁. Определите показания амперметра А₁ и вольтметра V₂

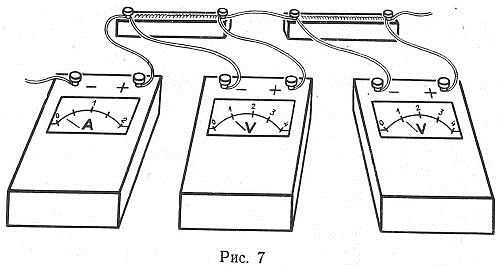
Иногда подобные задачи считают экспериментальными. С этим согласиться нельзя, если речь идет о задачах-измерителях.

Экспериментальная задача должна требовать предметной деятельности, а не работы с рисунками, схемами, фотографиями. Она или требует проведения эксперимента (опыта, наблюдения) для получения условий, необходимых для решения проблемы, или при заданных условиях требует проведения эксперимента или измерений для нахождения искомой величины. Экспериментальные задачи, как и любые другие, дают возможность проверить логику мышления, умение владеть математическим аппаратом и другие качества, которые в данной контролирующей ситуации важны, но не являются главными.

Так, ученик может безукоризненно провести все измерения, которые требуются для решения задачи, но ошибиться при подстановке их в формулу и поэтому получит неправильный числовой результат. Однако поэлементный анализ решения этой задачи позволит выявить отличные измерительные навыки ученика.

Так как экспериментальные задачи требуют предметной деятельности, в практике их часто не применяют. При контроле проще дать вычислительную задачу, чем экспериментальную, при решении которой необходимо специальное оборудование. Между тем практический навык проявляется только в практической деятельности. Приведем пример (VI класс).

На рис. 8 дано три мензурки. Определите объем жидкостей в мензурках 1 и 2. Нарисуйте уровень воды в мензурке 3, если объем воды в ней равен 170 мл.

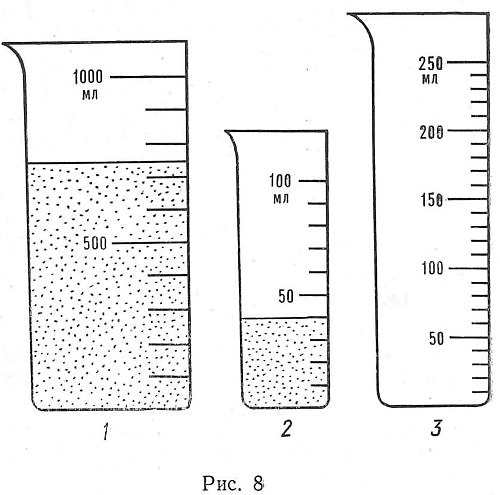
Ученик может правильно решить задачу по рисунку, но неправильно определять объем жидкости в ней на практике.

На первый взгляд это умение простое, однако оно требует некоторой практики в правильном расположении глаза при определении уровня жидкости относительно шкалы, чтобы избежать ошибки из-за параллакса. Сказанное не означает, что подобные задачи не следует применять в учебном процессе. Наоборот, они необходимы, но в контрольных работах их не следует называть экспериментальными.

Это задачи на мыслительный експеримент. Они выявляют умение ученика вообразить реальную ситуацию, опираясь на рисунки или описание в тексте, мысленно преобразовать ее и получить нужный результат. Это важное умение, но его не относят к практическим умениям.