Одномерные или линейные дефекты — дислокации

К этому классу дефектов относят нарушения кристаллической решетки, имеющие в одном из направлений большие (в пределе макроскопические) размеры, а в других направлениях малые размеры (в пределе— одно или несколько межатомных расстояний). Такие дефекты играют определяющую роль в механизме деформации и упрочнения кристаллических тел, и поэтому линейные дефекты заслуживают более подробного рассмотрения.

Выше рассматривались различные типы точечных дефектов м искажений кристаллической структуры. Для того чтобы установить принципиальные различия между линейными дефектами и другими типами нарушений, введем понятия «хорошего» и «плохого» кристалла. Во всех случаях, рассмотренных выше, атомы смещались из идеальных положений в решетке, но всегда можно было найти однозначное соответствие между каждым атомом в »искаженной решетке и соответствующим атомом в идеальном кристалле.

Для простоты будем рассматривать кристаллы с простой кубической структурой и сечения решетки, перпендикулярные плоскости (100). Участок сечения идеального кристалла для этого случая приведен на рис. 1.14, а. Построим в кристалле некоторый произвольный замкнутый контур, проходящий через узлы кристаллической решетки, и пронумеруем атомы, входящие в этот контур. Такой контур носит название контура Бюргерса.

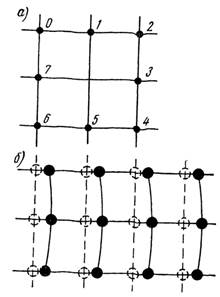
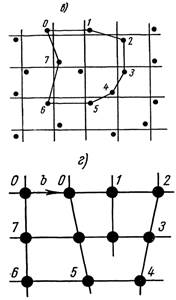
Рис. 1.14. Проекция кристалла с простои кубической структурой на плоскость (100). Контур Бюргерса: а) в идеальном кристалле, б) в упругодеформированном кристалле, в) в кристалле, атомы которого смещены из равновесных положений за счет теплового движения, г) в кристалле, содержащем краевую дислокацию

В упругодеформированном кристалле (рис. 1.14, 6) ряд атомов сдвинут из равновесных положений в решетке на различные расстояния, но если провести в нем контур Бюргерса такой же, как в идеальном кристалле, то вследствие однозначного соответствия между атомами в обеих решётках контур Бюргерса деформируется, но остается замкнутым.

В реальном кристалле, как указывалось выше, атомы смещены из узлов решетки вследствие теплового движения. В этом случае, как видно из рис. 1.14, в, контур Бюргерса тоже является замкнутым. Наконец, если в материале содержится точечный дефект, например вакансия, то атомы вокруг вакансии смещены, но контур Бюргерса остается замкнутым. Реальный кристалл, в котором контур Бюргерса любых размеров и формы остается замкнутым при повторении контура Бюргерса, проведенного в идеальном кристалле, носит название хорошего кристалла. К областям хорошего кристалла, как легко убедиться путем построения контура Бюргерса, относятся области, содержащие любые сложные точечные дефекты (дивакансия, кроудион и др.)

Создадим теперь линейный дефект, введя в кристаллическую решетку лишнюю полуплоскость, перпендикулярную плоскости чертежа (рис. 1.14, г). Построим контур Бюргерса так же, как это делалось на рис. 1.14, а—1.14,в (2 атома вправо, 2 атома вниз, 2 атома влево, 2 атома вверх). Как видно из рисунка, контур Бюргерса получился разомкнутым, с невязкой, равной одному межатомному расстоянию.

Если контур Бюргерса, окружающий некоторую область реального кристалла, имеет невязку по сравнению с соответствующим контуром для идеального, или хорошего кристалла, то эта область называется областью плохого кристалла. Дефект, расположенный в области плохого кристалла, называется дислокацией. Невязка контуров Бюргерса, проведенных в хорошем и плохом кристаллах, носит название вектора Бюргерса.

Таким образом, дислокацией называется линейный дефект кристаллической решетки, для которого вектор Бюргерса отличен от нуля. Как будет показано ниже, это определение является общим для большого класса дислокаций, а геометрическая схема, представленная на рис. 1.14, г, является частным случаем.

Из простых геометрических схем легко видеть, что изменение размера и формы контура Бюргерса, окружающего дислокацию, не влияет на величину вектора Бюргерса.

Необходимо отметить, что не только величина, но и направление вектора Бюргерса не зависит от места, в котором начинают строить контур Бюргерса. Из рассмотрения контура Бюргерса на рис. 1.14, г видно, что с какого бы из атомов, обозначенных цифрами от 0 до 7, мы не начинали построение, направление вектора Бюргерса не изменится. Следует отметить, что контур Бюргерса, который для простоты был на рис. 1.14, г проведен близко к краю лишней полуплоскости, в действительности следует проводить на достаточно далеком расстоянии от этого края так, чтобы искажения за счет дислокации не влияли на межатомные расстояния.

Поэтому место начала отсчета при проведении контура Бюргерса не играет роли и вектор Бюргерса (в рассматриваемом частном случае) равен межатомному расстоянию в направлении [100] в кристалле (величину такого межатомного расстояния будем обозначать b = a₁₀₀)

Далее очевидно, что такую же дислокацию, как приведенная на рис. 1.14, г, можно получить, вдвигая лишнюю полуплоскость не сверху, а снизу. Отличие между дислокациями в этом случае будет в знаке вектора Бюргерса. Следует отметить, что определение дислокации, обратное данному выше (а именно: если контур Бюргерса в реальном кристалле замкнут, то кристалл не содержит дислокации), вообще говоря, неверно, так как контур может охватывать несколько дислокаций, сумма векторов Бюргерса которых равна нулю.

Назовем край лишней полуплоскости линией дислокации. Из рассмотрения трехмерной схемы, сечение которой приведено на рис. 1.14, г, следует, что вектор Бюргерса является постоянным по всей длине дислокации, т. е. в бесконечном кристалле, содержащем одну дислокацию, линия дислокации не может оборваться внутри кристалла и дислокация должна образовывать замкнутую петлю.

В кристалле конечных размеров линия дислокации может выходить на поверхность кристалла, границу между кристаллами или границу инородного включения. Наконец, из приведенного выше примера равенства нулю суммарного вектора Бюргерса дислокаций противоположного знака видно, что векторы Бюргерса могут складываться по законам векторного анализа и сумма векторов Бюргерса дислокаций, встречающихся в узле, равна нулю. Таким образом, дислокации могут обрываться и на других дислокациях. Доказательства перечисленных свойств контура и вектора Бюргерса приведены в книге Рида.

Классификация дислокаций основана на зависимостях между направлениями вектора Бюргерса и линии дислокации и соотношениях между величинами вектора Бюргерса и межатомных расстояний в кристалле. Как видно из рис. 1.14, г, для дислокации, изображенной на этой схеме, величина вектора Бюргерса равна межатомному расстоянию. Дислокации такого типа называются полными. Из той же схемы видно, что направления вектора Бюргерса и линии дислокации взаимно перпендикулярны. Такие дислокации носят название краевых.

При образовании краевой дислокации кристалл разрезался и в разрез вставлялась дополнительная полуплоскость. Другой вид дислокации образуется в том случае, если после разрезки сдвинуть одну половину кристалла относительно другой. Построение контура Бюргерса и сравнение его с контуром Бюргерса в идеальном кристалле показывает существование невязки контура; следовательно, этот дефект является дислокацией. Как линия дислокации, так и контур Бюргерса в этом случае направлены вдоль вертикальной оси.

Дислокации, для которых линия дислокации и вектор Бюргерса параллельны, носят название винтовых; дислокации промежуточного типа называются смешанными. В простой кубической структуре при сечении по плоскости (100) винтовая дислокация может быть изображена, если рассматривать две (последовательных атомных плоскости. Соответствующая схема приведена на рис. 1.15.

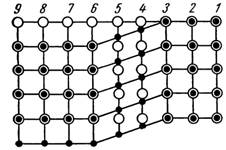
Рис. 1.15. Проекция двух последовательных плоскостей (100) в кубическом кристалле, содержащем винтовую дислокацию

Атомы верхнего слоя на рисунке изображены кружками, атомы нижнего слоя — точками (вектор Бюргерса направлен вертикально, линия дислокации также направлена вертикально).