Масштаб, проекция, системы координат

В определении карты сказано, что одним из важнейших ее свойств является математический закон построения. Он проявляется в наличии масштаба и картографической проекции.

Масштабом называется отношение длины линии на карте к длине соответствующей линии на земном шаре. Масштаб показывает, во сколько раз уменьшено картографическое изображение, сколько сантиметров на местности содержится в одном сантиметре на карте. Например, масштаб 1:1 000 000 означает, что 1 см на карте соответствует 1 000 000 см на местности, т. е. 10 км. На картах дают не только числовой, но и линейный масштаб — отрезок масштабной линейки, удобной для выполнения измерений.

Картографическая проекция — это способ перехода от реальной, геометрически сложной земной поверхности к плоскости карты. Для этого вначале переходят к математически правильной фигуре эллипсоида или шара, а затем проектируют изображение на плоскость опять-таки с помощью строгих математических зависимостей. В результате каждой точке на земном шаре с широтой ȹ и долготой λ соответствует одна и только одна точка на карте с прямоугольными координатами х и у. Поэтому общее уравнение картографических проекций имеет вид:

Сферическую поверхность невозможно развернуть на плоскость без деформаций — сжатий и растяжений. Значит, всякая карта имеет те или иные искажения. Различают искажения длин, площадей, углов и форм. На крупномасштабных картах искажения могут быть практически неощутимы, но на мелкомасштабных они бывают очень велики. Картографические проекции обладают разными свойствами в зависимости от характера и размера искажений.

Равноугольные проекции сохраняют без искажений углы и формы малых объектов, зато в них резко деформируются длины и площади объектов. По картам в равноугольных проекциях удобно, например, прокладывать маршруты судов и самолетов, но невозможно измерять площади.

Равновеликие проекции не искажают площадей, но углы и формы объектов в них сильно искажены. Эти проекции хорошо приспособлены для определения площадей (например, размеров государств, земельных угодий и др.).

Произвольные проекции имеют искажения длин, площадей и углов, но они распределяются по карте наиболее выгодным образом. Например, выбирают проекции с минимальными искажениями в центральной части, зато они резко возрастают по краям карты. Среди произвольных проекций выделяются равнопромежуточные, в которых искажения длин отсутствуют по одному из направлений: либо вдоль меридиана, либо вдоль параллели.

Проекции различают и по виду вспомогательной поверхности, используемой при переходе от эллипсоида или шара к плоскости карты. Наиболее распространены проекции цилиндрические, когда проектирование с шара ведется как бы на поверхность цилиндра, конические и поликонические, когда вспомогательными поверхностями служат один или несколько конусов и азимутальные, когда проектирование ведется на плоскость рис. 109. Кроме того, существует большой класс условных проекций, при построении которых не пользуются геометрическими аналогиями, а лишь математическими уравнениями нужного вида.

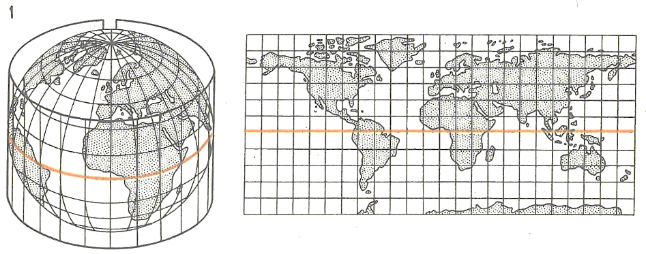
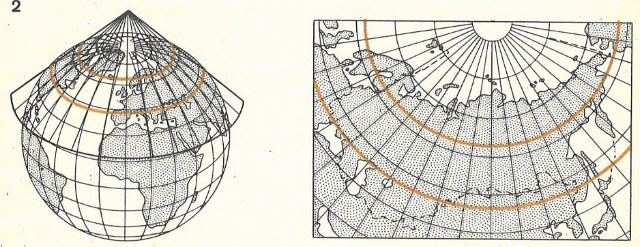
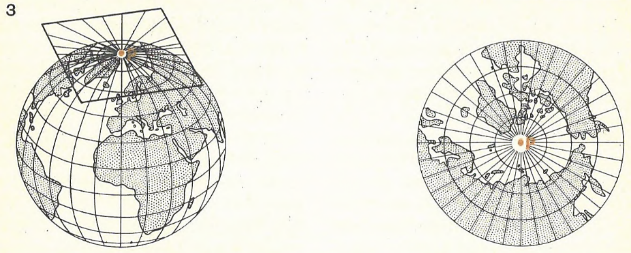
Рис. 9. Картографические проекции: 1. Цилиндрическая проекция. 2. Коническая проекция. 3. Азимутальная проекция. Выделены линии и точки нулевых искажений, где происходит касание или сечение шара вспомогательной поверхностью. На этих линиях и в точках сохраняется главный масштаб

Для карт мира чаще всего применяют цилиндрические и различные условные проекции рис. 110 обладающие наименьшими искажениями в области экватора и средних широт. Для карт СССР обычно выбирают конические проекции, в которых воображаемый конус сечет земной шар по параллелям 47° и 62° с. ш., - это так называемые линии нулевых искажений. Вблизи них искажения невелики.

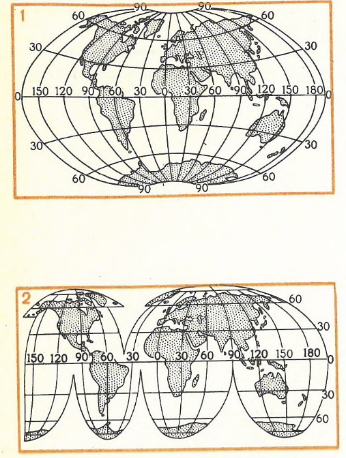
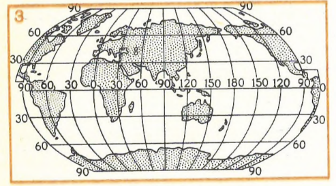
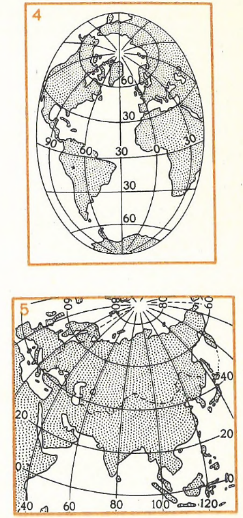
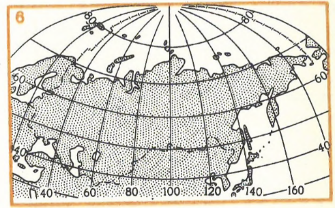
Рис. 110. Некоторые картографические проекции для карт мира, материков, океанов СССР: 1. Поликоническая проекция для карты мира. Применяется для изображения материков, небольшие искажения площадей сохраняются в центральной части. 2. Проекция с разрывами для карты Мира. Имеет малые искажения в пределах материков за счет разрывов изображения на океанах. 3. Псевдоцилиндрическая проекция для карты Мира. Удобна для цельного изображения Тихого, Атлантического и Индийского океанов.

4. Условная овальная проекция. Применяется для совместного показа Атлантического и Северного Ледовитого океана, имеет небольшие искажения площадей. 5. Косая азимутальная проекция для карты Азии с сопредельными районами. Не имеет искажений площадей. 6. Косая перспективно-цилиндрическая проекция для карты СССР. Отличается наглядностью, хорошо передает сферичность земной поверхности

Это удобно, поскольку между указанными параллелями размещаются основные хозяйственные зоны нашей страны и здесь сосредоточена максимальная нагрузка карт.

Зато в конических проекциях сильно искажаются районы, лежащие в высоких широтах и акватории Северного Ледовитого океана.

На мелкомасштабных картах главный масштаб (тот, что указан на карте) сохраняется только на линиях и в точках нулевых искажений, там, где вспомогательная поверхность касается (или сечет) шар. Во всех остальных частях карты масштаб несколько преувеличен или преуменьшен. Для определения частного масштаба в любом месте карты проводят специальные расчеты. При этом нужно знать длину какой-либо линии на шаре (например, расстояние между двумя городами, длину отрезка меридиана или параллели) и ту же длину на карте.

Географические координаты — угловые величины: широта и долгота, определяющие положение любой точки относительно экватора и начального (Гринвичского) меридиана. Широтой точки называется угол между плоскостью экватора и отвесной линией в данной точке. Долготой называется линейный угол двугранного угла, образованного плоскостью начального меридиана и плоскостью меридиана, проходящего через данную точку рис. 111.

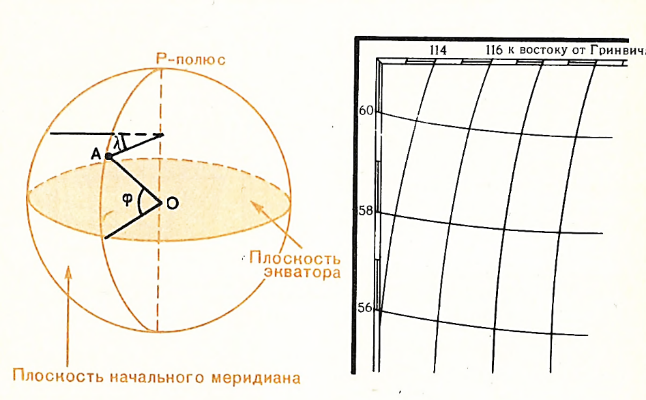
Рис. 111. Географические координаты. Широта (ȹ) и долгота (λ) на глобусе. Сетка меридианов и параллелей на карте

На карту наносятся линии параллелей и меридианов. Параллель — это любая линия, все точки которой имеют одну и ту же географическую широту. Счет параллелей идет от экватора к северу и югу (от 0° до 90° с. ш. или ю. ш.). Меридиан — это линия, все точки которой имеют одинаковую географическую долготу. По отношению к Гринвичскому меридиану различаются западные и восточные долготы (з. д. и в. д.), отсчитываемые от 0° до 180°.

Линии меридианов и параллелей образуют картографическую сетку. Обычно на рамках карты подписывают значения меридианов и параллелей и дают более дробные деления (например, через 5° или через 1°) для удобства отсчета координат.

Прямоугольные координаты — система координат, в которой за ось абсцисс (X) принят осевой меридиан 6-градусной геодезической зоны, а за ось ординат (У) — экватор рис. 112. Точка пересечения осевого меридиана и экватора (начало координат) имеет значения: Х = 0 км; У = 500 км. Это сделано для того, чтобы в пределах каждой зоны не было отрицательных значений У. Величины X всегда положительны, так как территория СССР расположена к северу от экватора.

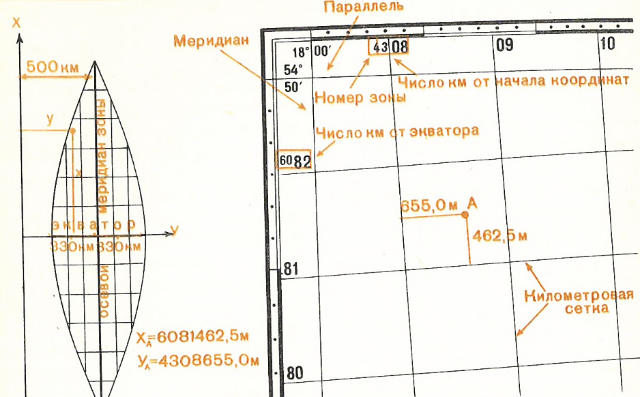
Рис. 112. Прямоугольные координаты. Изображение геодезической зоны с координатными линиями и километровая сетка на топографической карте

На топографические карты нанесены линии, проведенные через 1 км и параллельные осям X и У. Они образуют квадратную километровую сетку, которая служит для снятия с карты прямоугольных координат объектов или нанесения объектов по их координатам. У рамок карты подписаны значения линий километровой сетки в целых км. Для координат У указан также номер зоны. Например, координата X = 6 081 462,5 означает, что точка удалена от экватора на 6081 км и 462,5 м, а У = 4 308 655,0 показывает, что точка находится в 4-й зоне и имеет координату 308 км и 655 м, т. е. удалена к западу от осевого меридиана на 191 км 345 м.

Сетка прямоугольных координат наносится только на топографические карты и используется при выполнении различных геодезических работ, вычислении по картам расстояний, направлений, площадей объектов.