Идеальные кристаллы. Индексы плоскостей и направлений

Возможны различные пути рассмотрения кристаллических тел. Некоторые общие свойства кристаллов (например, плотность) удобно рассматривать, если считать кристалл непрерывной сплошной средой (изотропным континуумом).

Другие свойства, например, упругость, целесообразно рассматривать, применяя несколько усложненное представление о кристалле как непрерывной сплошной среды, свойства которой зависят от направления (анизотропном континууме). Наконец, рассмотрение атомной структуры кристалла требует представления о нем как о прерывной среде с трехкратным периодическим распределением вещества (однородном дисконтинууме).

Это последнее представление удобно использовать при рассмотрении механизма пластической деформации кристаллов.

Рассмотрим кратко симметрию и некоторые кристаллографические характеристики наиболее распространенных материалов. (Более подробное изложение этих вопросов приведено, например, в книге Г. С. Жданова [1].) В каждом случае будем рассматривать форму элементарной ячейки, повторение которой в пространстве позволяет заполнить объем. Атомы будем моделировать равновеликими несжимаемыми шарами одинакового радиуса, притягивающимися друг к другу.

Это приближение достаточно точно для описания структуры кристалла, если межатомные связи являются ненаправленными и ненасыщенными, что справедливо, например, для атомов металлов. Если межатомные связи являются направленными и насыщенными, то их моделируют шариками с рядом продолженных радиусов, изображающих линии связи. К структурам, состоящим из атомов такого типа, относятся, например, структуры германия, кремния и графита.

Для данной кристаллической решетки исчерпывающими характеристиками семейства атомных плоскостей являются ориентировка одной из этих плоскостей относительно выбранных осей координат, а также расстояние между ближайшими параллельными плоскостями. Расстояния между идентичными атомами но осям координат х₁ х₂, х₃ обозначим соответственно а, b и с. Пусть ближайшая к началу координат плоскость рассматриваемого семейства отсекает на осях решетки отрезки а/h, b/k, с/l, причем, как легко показать, h, k и l всегда являются целыми числами. Величины (hkl) называются индексами плоскости и записываются в круглых скобках. Например, плоскость (211) отсекает на осях.

координат отрезки а/2, b, с. Если плоскость отсекает на осях отрицательные отрезки, то это отмечается знакам минус над соответствующим индексом. Очевидно, что любая плоскости отсекающая по осям координат отрезки, в целое число раз больше приведенных, принадлежит к тому же семейству плоскостей. Кроме того, изменение знаков у всех индексов на обратные не меняет ориентации плоскости в пространстве. Совокупность всех возможных сочетаний индексов при фиксированных величинах (с учетом изменений знака) описывает некоторый многогранник в. пространстве и обозначается {hkl}.

Каждое направление в кристаллической решетке однозначно определяется координатами первого атома на прямой, проведенной в этом направлении из начала координат. Семейство направлений характеризуется индексами направлений [uvw], которые пишутся в квадратных скобках. Совокупность сочетаний индексов направлений обозначается (uvw). Ниже будут рассмотрены элементарные ячейки — призмы минимального размера в решетке, симметрия которых хорошо соответствует симметрии свойств кристалла.

В табл. 1 приведены основные характеристики элементарных ячеек кубической, гексагональной и тетрагональной систем; в которых кристаллизуется большинство веществ, рассматриваемых в физической теории прочности и пластичности.

Отметим, что для гексагональной системы элементарная ячейка,, строго говоря, является параллелепипедом с а = b ≠ с, a=ß = 90°, γ =120°; но при таком описании менее наглядна симметрия кристалла.

На рис. 1.1 приведены индексы некоторых плоскостей и направлений в элементарной ячейке кубической системы.

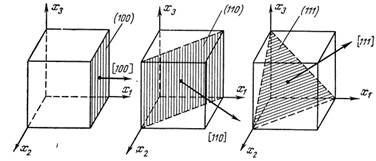
Рис. 1.1. Индексы плоскостей и направлений в кубической системе

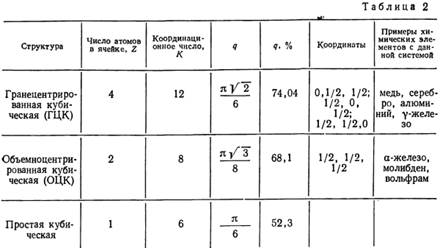
Расположение атомов в реальных кристаллических телах имеет в действительности несколько более сложный характер. В табл. 2 приведены координаты дополнительных атомов (кроме атомов, находящихся в вершинах элементарной ячейки) для основных структурных типов кубической и гексагональной систем, в которых кристаллизуются химические элементы.

На рис. 1.2, а — 1.2, в приведены схемы элементарных ячеек для этих структур. Рассмотренные структуры характеризуют практически все элементы, для которых имеют значения их пластические и прочностные свойства. В этом легко убедиться из анализа распределения элементов, входящих в периодическую систему Д. И. Менделеева, по кристаллическим структурам [1].

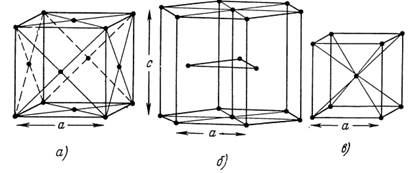
Рис. 1.2. Элементарные ячейки некоторых структурных типов: а) гранецентрированная кубическая структура; б) гексагональная плотноупакованная; в) объемноцентрированная кубическа

Среди элементов левых подгрупп периодической системы преобладают структуры:
- гранецентрированная кубическая,
- гексагональная плотноупакованная,
- кубическая объемноцентрированная,
- алмазная.
Элементы правых подгрупп имеют более сложные структуры.

При определении индексов плоскостей и направлений в гексагональной системе часто добавляют четвертую ось, обозначаемую через Оu, направляя ее в плоскости (х₁Oх₂) под углом 120° к осям Ох₁ и Ох₂ и задавая вдоль этой оси масштаб, равный а. Символ грани или системы плоскостей решетки при этом записывается так же, как прежде, за исключением того, что теперь он содержит четыре индекса, т. е. в общем случае (hkil), где индекс і относится к оси Оu.

Индексы h, k, і зависят друг от друга; можно показать, что они связаны соотношением h + k + i = 0. Преимущество использования четырех осей состоит в том, что кристаллические грани одной и той же формы, скажем {hkil}, обозначаются совокупностями индексов, которые, если не считать знаков, получаются одна за другой простой перестановкой индексов; таким образом, это правило становится общим для всех систем.

Такие обозначения необходимо отличать от трехиндексных, описанных выше. Направление, как и грань, обозначается в этом случае системой чисел [u'v’t'w'] причем сумма первых трех из них равна нулю, т. е. u'+v'+t'=0.

В четырехиндексном обозначении ось Ox₁ имеет символ [2110], в то время как в трехиндексном обозначении — символ [100]. Таким образом, символы одного и того же направления в двух обозначениях (выглядят совершенно различно.