Уравнение множественной регрессии
Аналитическим выражением многофакторных связей являются уравнения множественной регрессии. В рассматриваемом примере, предложенном Г. Н. Зайцевым о высоте растений, массе 1000 семян и урожайности сои связь между факторами оказалась недостаточно тесной (табл. 19). В данном случае целесообразно искать параметры уравнения, выражающего зависимость массы семян от двух других факторов:
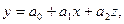 где у- функция, зависимая переменная, масса 1000 семян; а0, а1, а2 – коэффициенты уравнения; х – высота растений (в см) и z- урожайность сои (в ц/га)- независимые переменные.
где у- функция, зависимая переменная, масса 1000 семян; а0, а1, а2 – коэффициенты уравнения; х – высота растений (в см) и z- урожайность сои (в ц/га)- независимые переменные.
Таблица 20
Зависимость массы 1000 семян (у) от высоты растений (х)
и урожайности (z) у сои (у, - теоретические значения массы семян)
| х, см | z, ц/га | у, г | у,, г | х - Мх | z - Mz | y- My |
| 214,3 | 1,462 | -4 | -21,62 | |||
| 208,3 | -20,538 | -3 | -20,62 | |||
| 216,5 | 12,462 | -5 | -10,62 | |||
| 220,1 | -1,538 | -8,62 | ||||
| 218,0 | -2,538 | -1 | -3,62 | |||
| 210,0 | 8,462 | -8 | -2,62 | |||
| 225,5 | -0,538 | -2,62 | ||||
| 235,8 | 9,462 | 2,38 | ||||
| 218,4 | -1,538 | -1 | 4,38 | |||
| 232,4 | 9,462 | 13,38 | ||||
| 225,4 | -10,538 | 14,38 | ||||
| 221,5 | -21,538 | 14,38 | ||||
| 221,7 | 17,462 | -3 | 21,38 | |||
| +0,006 | 0,06 |
Для получения коэффициента уравнения множественной регрессии требуется, например, по предлагаемому способу, решить систему трех
нормальных уравнений, полученных по методу наименьших квадратов:
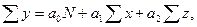
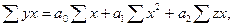
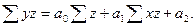
Для решения уравнений вычислим необходимые суммы (Табл.21).
Таблица 21
Дата добавления: 2020-10-25; просмотров: 668;











