Анализ корреляционной зависимости массы семян (у) от продолжительности вегетации (х) у сортов ячменя
| х у | ny | ay | |||||||
Продолжение табл. 16
| nx | N=214 | ||||||||
| ∑fay | |||||||||
| (∑fay)2/nx | 12,50 | 304,69 | 489,44 | 761,29 | 1160,12 | 136,13 | 72,25 | 2936,42 | |
| ax | |||||||||
| (∑fay)/nx | 2,50 | 3,24 | 3,79 | 3,48 | 3,96 | 4,13 | 4,25 | ||
| у/х | 37,00 | 41,44 | 44,74 | 42,88 | 45,76 | 46,78 | 47,50 |
2. Суммируем частоты по столбцам (nx) и по строкам (ny).
3. Записываем условные отклонения ах и ау от начала рядов х и у в виде натурального ряда чисел, начиная с 0, соответственно направлению возрастания вариант в обоих рядах.
4. Получаем по столбцам произведений частот на соответствующие им условные отклонения ау: первая сумма 5= 1 х 3 + 1 х 2; последняя сумма 17 = 2 х 5 + 1 х 4 + 1 х3. В итоге этой строки ∑fay=790.
5. Значения ∑fay возводим в квадрат и делим каждое из них на соответствующие им суммы частот (∑fay)/nx , получаем: 12,50; 304,69; 489,44 и т.д., в итоге этой строки: 
6. Для получения точек эмпирической линии регрессии отдельные значения ∑fay: 5,94; 129 и т.д. надо разделить на соответствующие им nх: 2,29; 34 и т.д. В результате получим (∑fay)/ nх: 2,50; 3,24; 3,79 и т.д. Каждое из полученных значений умножается на величину классового интервала и к каждому произведению прибавляется минимальная варианта ряда у, равная для нашего примера 22: 2,50 х 6 +22=37,00; 3,24 х6 +22= 41,44; 3,79 х 6 +22 =44,74 и т.д. Полученные значения у/х представляют собой точки эмпирической линии регрессии.
7. Перемножаем все значения n на соответствующие условные отклонения ах и складываем произведения: 2 х 0 +29 х 1 + 34 х 2 +63 х 3 +…+4 х6 =646 = 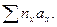
8. Получаем сумму 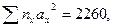 перемножая значения nх на квадраты условных отклонений: 2 х 02+29 х 12+34 х 22+ 63 х 32…и т.д.
перемножая значения nх на квадраты условных отклонений: 2 х 02+29 х 12+34 х 22+ 63 х 32…и т.д.
9. Подобно действиям в пунктах 7 и 8, получаем суммы:
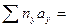 790= 1 х 0 + 6 х 1 + 26 х 2 …. и т.д.;
790= 1 х 0 + 6 х 1 + 26 х 2 …. и т.д.;
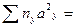 3222 = 1 х 02+ 6 х 12 + 26 х 22 + 58 х 32 и т.д.
3222 = 1 х 02+ 6 х 12 + 26 х 22 + 58 х 32 и т.д.
10. Получаем сумму 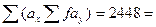 0 х 5 + 1 х 94 + 2 х 129 + 3 х 219 + 4 х 293 + 5 х 33 + 6 х 17.
0 х 5 + 1 х 94 + 2 х 129 + 3 х 219 + 4 х 293 + 5 х 33 + 6 х 17.
11. Подставляем найденные суммы в формулы:
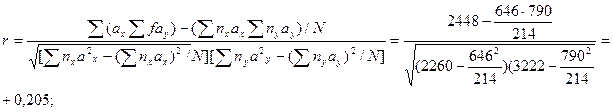
r2=0,0422;
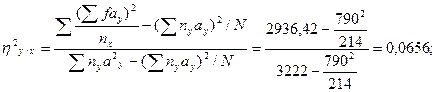
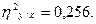
12. Оценку найденных показателей производим по критерию Фишера. Достоверность коэффициента детерминации (квадрата коэффициента корреляции) определяется по формуле 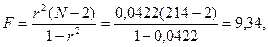
где F – критерий Фишера; r- коэффициент корреляции; N – объем выборки. Числа степеней свободы при оценке коэффициента детерминации принимаются: 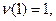 а
а 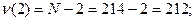 отсюда табличные значения критерия Фишера при Р1=95% равно 3,89. Вычисленные значения критерия больше табличного, поэтому можно сделать вывод о существовании достоверной прямолинейной зависимости массы 1000 семян от продолжительности вегетационного периода у сортов ячменя.
отсюда табличные значения критерия Фишера при Р1=95% равно 3,89. Вычисленные значения критерия больше табличного, поэтому можно сделать вывод о существовании достоверной прямолинейной зависимости массы 1000 семян от продолжительности вегетационного периода у сортов ячменя.
Достоверность квадрата корреляционного отношения определяется по формуле:
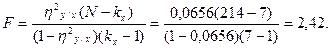
где F- критерий Фишера; 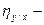 прямое корреляционное отношение; N- объем выборки; k- число классов в ряду х. Числа степеней свободы при определении достоверности
прямое корреляционное отношение; N- объем выборки; k- число классов в ряду х. Числа степеней свободы при определении достоверности 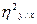 - принимается равными числу классов ряда х без единицы:
- принимается равными числу классов ряда х без единицы: 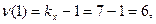 и объем выборки минус число классов ряда х:
и объем выборки минус число классов ряда х: 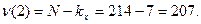
Отсюда при Р1=95% находим F1- табличное, равное 2,14. Вычисленное значение больше табличного, поэтому можно сказать о достоверности также и криволинейной зависимости массы плодов от продолжительности вегетации сортов ячменя.
Критерий криволинейности может быть вычислен разными способами. Приведем наиболее простой способ. Оценка степени криволинейности корреляционной зависимости , т.е. критерий криволинейности определяется по формуле: 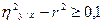 . Связь считается криволинейной, если разность квадратов больше 0,1. Для нашего примера
. Связь считается криволинейной, если разность квадратов больше 0,1. Для нашего примера 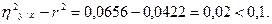
Таким образом, в нашем случае связь между массой зерен и периодом вегетации можно считать прямолинейной.
Оценка степени криволинейности связи при помощи критерия Стьюдента производится по формуле:
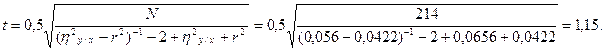 Вычисленное значение меньше трех и меньше табличного при Р=95%, которое равно 1,960, поэтому следует считать, что рассматриваемая связь несущественно отклоняется от прямолинейной.
Вычисленное значение меньше трех и меньше табличного при Р=95%, которое равно 1,960, поэтому следует считать, что рассматриваемая связь несущественно отклоняется от прямолинейной.
РЕГРЕССИЯ
После установления наличия корреляционной связи между двумя явлениями (признаками), следует выявить закономерность количественного изменения одного из признаков (функция) при изменении другого (аргумент). Такая закономерность необходима для прогноза изучаемого явления и выяснения его критических точек. Для этого изучаемую связь необходимо выразить аналитически в виде уравнения регрессии и графически – с вычислением точек кривой по установленному уравнению. При решении этих вопросов существенно снижается трудоемкость расчетов, путем преобразования исходных данных таким образом, чтобы их величины приближались, по возможности, к первому порядку. Для этого исходные данные делятся на одно и то же число, или вычисляется из них среднее или начальное значение, а также принимаются другие единицы измерения.
Дата добавления: 2020-10-25; просмотров: 792;











