Суммы квадратов и произведений высоты, массы и урожайности

Продолжение табл. 21

∑ y = 2868, ∑x=839, ∑yx=185412, ∑x²=55969, ∑yz = 57737, ∑xz = 16609, ∑z²= 5458, ∑z = 260.

1.Подставим полученные суммы в выше приведенную систему уравне-ний:

(1) 2868 = 13а₀ + 839а₁ + 260а₂,

(2) 185412 = 839а₀ + 55869а₁ +16609а₂,

(3) 57737 = 260а₀ +16609а₁ + 5458а₂.

2.Решим систему, состоящую из первого и второго уравнений, для чего разделим первое уравнение на 13, а второе – на 839 и вычтем из второго первое:

220,9916 = а₀ + 66,589 а₁+ 19,7962 а₂

-

220,6154 = а₀ + 64,5385 а₁ + 20а₂

0,3762 = 2,0515 а₁ – 0,2038а₂

3. Чтобы получить второе уравнение с двумя неизвестными, решим систему, состоящую из первого и третьего уравнений, для чего разделим первое уравнение на 13, а третье на 260 и вычтем из третьего первое:

222,0654 = а₀ + 63,8808 а₁+ 20,9923 а₂

-

220,6154 = а₀+ 64,5385 а₁ + 20а₂

1,4500= - 0,6577а₁+ 0,9923 а₂

4. Решим систему двух получившихся уравнений с двумя неизвестными:

0,3762 = 2,0515 а₁ – 0,2038а₂

1,4500= - 0,6577а₁+ 0,9923 а₂

для чего разделим первое из них на 2,0515, а второе – на 0,6577 и, сложив полученные уравнения, найдем а₂:

0,183378 = а₁ – 0,099342 а₂

+

2,20465 = -а + 1,50874 а₂

2,388028 = 1,409398 а₂

а₂ = 1,694367

5. Подставляя значения а₂ в первое уравнение из системы двух уравнений (пункт 4) с двумя неизвестными, определим а₁:

0,3762 = 2,0515 а₁ – 0,2038 х 1,6944;

а₁ = (0,3762 + 0,3453)/2,0515 = 0,3517.

6. Подставляя в первое уравнение нашей начальной системы значения а₁ и а₂, найдем а₀:

2868 = 13а₀+ 839 х 0,3517 + 260 х 1,6944;

а₀ = (2868 – 295,0763 – 440,5440)/ 13 = 164,030.

7. Уравнение регрессии:

y_xz = 164,030 + 0,3517x + 1,69436z.

8. Проверка: подставляя в первое уравнение начальной системы значения а₀, а₁ и а₂, получим:

2868 + 13х 164,030 +839 х 0,3517 + 260 х 1,69436 = 2132,3900 + 295,0763 + 440,5336 = 2867,9999.

Очевидно, что коэффициенты а₀, а₁ и а₂ определены правильно.

9. Ошибка уравнения множественной регрессии определяется по формуле:

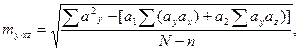
где 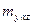- ошибка теоретических значений функции у; a_y, a_x, a_z – коэффициенты уравнения множественной регрессии; N – объем ряда; n – число коэффициентов уравнения, включая свободный член.

Суммы отклонений a_y, a_x, a_z вычисляются по формулам:

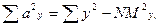
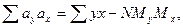
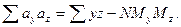
Пользуясь данными табл.20, определяем средние арифметические рядов x, y, z по формуле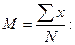

М_х = 839/13=64,5384; М_у=2868/13 =220,615; М_z=260/13=20,0;

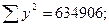
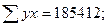
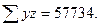
Подставляя найденные величины в формулы сумм отклонений

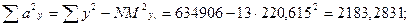
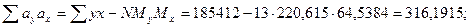
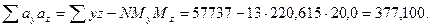
Определены все величины, необходимые для вычисления ошибки уравнения множественной регрессии по формуле:

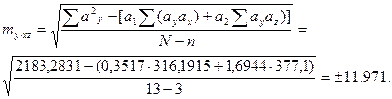
Таким образом, по уравнению у_xz= 164,030 +0,3517_х +1,6944_z, можно рассчитать массу 1000 семян, зная высоту растений и урожайность сои с ошибкой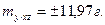

Коэффициенты уравнения множественной регрессии можно найти и другими способами, например, через суммы квадратов и произведений отклонений от средней. При этом, несколько сокращается трудоемкость расчетов, так как позволяет оперировать с меньшими по абсолютной величине числами. Способ может применяться в любых случаях, но особенно он рекомендуется тогда, когда исходные данные представлены многозначными числами, а также когда одновременно желательно вычислить дисперсии, сигмы всех трех рядов и коэффициенты корреляции между ними. Рассмотрим технику вычисления, используя тот же пример, что и в первом способе (Табл. 22).

Таблица 22