Вычисление сумм для определения коэффициентов уравнения множественной регрессии (Зайцев, 1984)

<18 19 202122 23 24 >

(х-М_х)²	(у-М_y)²	(z-M_z)²	(х-М_х) (у-М_y)	(z-M_z) (у-М_y)	(х-М_х) (z-M_z)

2,1374	467,42		-31,608	86,48	-5,848

Продолжение табл. 22

421,81	425,18	423,49	61,86	61,614
155,3	112,78	-132,35	53,1	-62,31
2,3654	74,304	13,258
6,4414	13,104	9,1876	3,62	2,538
71,605	6,8644	-22,17	20,96	-67,696
0,28944	6,8644	1,4096	-7,86	-1,614
89,529	5,6644	22,52	16,66	66,234
2,3654	19,184	-6,7364	-4,38	1,538
89,529	179,02	126,6	66,9	47,31
111,05	206,78	-151,54	71,9	-52,69
463,89	206,78	-309,72	71,9	-107,69
304,92	457,1	373,34	-64,14	-52,386

1721,2

2181,2

315,68

-171

1. По данным табл. 19 вычислим средние арифметические для трех вариационных рядов: М_у=220,62; М_х=64,538; M_z=20; и следующие суммы (табл.21):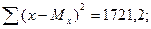

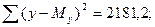
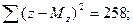
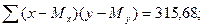
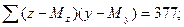
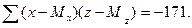
2. Найдем вспомогательные величины:

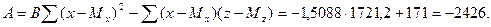
3.Коэффициент при х равен:

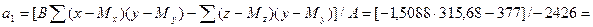
0,35173.

4. Коэффициент при z равен:

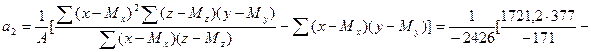
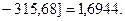
5.Находим свободный член уравнения множественной регрессии:

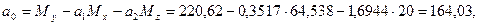
таким образом, величины всех коэффициентов практически совпадают с полученными ранее. Используя суммы из табл.21, можно вычислить сигмы всех трех рядов и коэффициенты корреляции между ними по формулам:

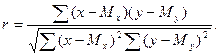
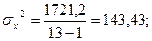
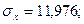
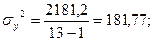
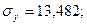
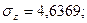
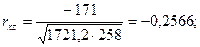
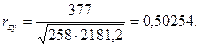
Коэффициенты корреляции между этими признаками совпадают с величинами коэффициентов, вычисленными другими способами.

Оценку достоверности значений коэффициентов, или, точнее, оценку достоверности их отличия от нуля, можно произвести по формулам:

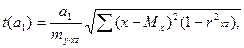
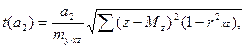
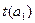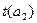где и - величины критерия Стьюдента, сравниваемые с табличными значениями, при числе степеней свободы: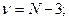 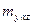- ошибка уравнения по формуле: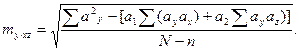

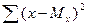и 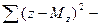суммы квадратов отклонений величин x и z;

r_xz- коэффициент корреляции между рядами x и z. Величина критерия Стьюдента соответственно для коэффициентов а₁ и а₂ равна:

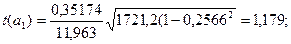
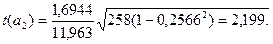
При числе степеней свободы 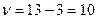и на 95% доверительном уровне t =2,228, что больше вычисленных значений. Следовательно, можно сделать заключение, что масса семян сои (у) существенно не зависит ни от средней высоты растений (х), ни от урожайности (z).