Анализ корреляционной зависимости массы семян (у) от продолжительности вегетационного периода (х) у сортов ячменя (по Г. Н. Зайцеву, 1984)

х: у								ny	ay
nx								N=214
∑fay
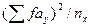
	12,50	304,69	489,44	761,29	1160,12	136,13	72,25	2936,42

Продолжение табл. 15

ax									∑n xа x2 2260
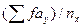
	2,50	3,24	3,79	3,48	3,96	4,13	4,25
y/x	37,00	41,44	44,74	42,88	45,76	46,78	47,50

2. Суммируем частоты по столбцам (n_x) и по строкам (n_y).

3. Записываем условные отклонения а_х и а_у от начала рядов х и у в виде натурального ряда чисел, начиная с 0, соответственно направлению возрастания вариант в обоих рядах.

4.Получаем по столбцам суммы произведений частот на соответствующие им условные отклонения а_у: первая сумма 5= 1 х 3 + 1 х 2; последняя сумма 17 = 2 х 5 + 1 х 4 + 1 х 3. В итоге этой строки ∑fa_y = 790.

5.Значения ∑fa_y = 790 возводим в квадрат и делим каждое из них на соответствующие им суммы частот 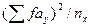, получаем: 12,50; 304,69; и т.д., в итоге этой строки получаем по формуле:

6. Для получения точек эмпирической линии регрессии отдельные значения 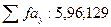и т. д. надо разделить на соответствующие им n_x: 2, 29, 34 и т.д. В результате получим 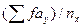: 2,50; 3,24 и т.д. Каждое из полученных значений умножается на величину классового интервала С=6 и к каждому произведению прибавляется минимальная варианта у = 22: 2,50 х 6 +22 = 37,00; 3,24 х 6 + 22 = 41Б44 и т.д. Полученные значения у/х представляют собой точки эмпирической линии регрессии.

7. Перемножаем все значения n на соответствующие условные отклонения а_х и складываем произведения: 2 х 0 + 29 х 1 + 34 х 2 +63 х 3 + …+ 4 х 6 = ∑n_xa_x.

8. Получаем сумму ∑n _x a_x²=2260, перемножая значения n_x на квадраты условных отклонений: 2 х 0² + 29 х 1² … и т.д.

9. Получаем суммы в результате действий, аналогичных пунктам 7 и 8:

∑ n _y a_y = 790 = 1 x 0 + 6 x 1 … и т.д.

∑ n _y a²_у = 3222 = 1 x 0² + 6 x 1² + 26 х 2² …и т.д.

10. Вычисляем сумму 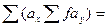2448 = 0 х 5 + 1 х 94 + 2 х 129 … и т.д.

11. Подставляя найденные значения в формулы, получим:

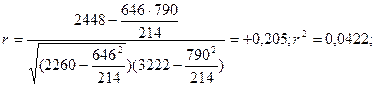
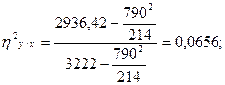
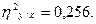
12. Оценку показателей производим по критерию Фишера.

Достоверность коэффициента детерминации (квадрата коэффициента корреляции) определяется по формуле: 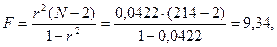где F – критерий Фишера; r- коэффициент корреляции; N - объем выборки.

Числа степеней свободы при оценке коэффициента детерминации принимаются: 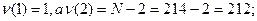отсюда табличное значение критерия Фишера при P₁=95% равно 3,89. Вычисленное по формуле критерий больше табличного, что показывает на существование достоверной прямолинейной зависимости массы зерен от продолжительности Вегетации.

Достоверность квадрата корреляционного отношения определяется по формуле: 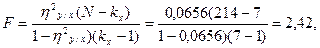где F- критерий Фишера; 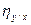- прямое корреляционное отношение; N- объем выборки; k_x- число классов в ряду х.

Число степеней свободы при определении достоверности 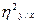по таблице принимаются равными числу классов ряда х без единицы: 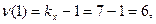и объему выборки минус число классов ряда х: 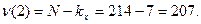При Р₁= 95% F табличное составляет 2,14. Вычисленное значение критерия – 2,42, что больше табличного, следовательно наблюдается и криволинейная зависимость между массой зерен и продолжительностью вегетационного периода у сортов ячменя.