Рекуррентные уравнения ПИД – регулятора

С этой целью по аналогии с выражением составим выражение для 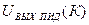в предыдущий ( 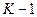) шаг квантования:

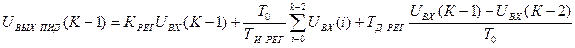.(10)

После вычитания выражения (10) из выражения (9) получим:

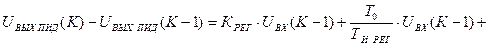
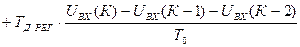. (11)

В уравнении (11) приращение интегральной составляющей равно:

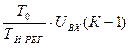. (12)

Изменение дифференциальной составляющей определяется по выражению

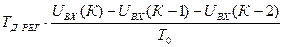. (13)

Значение 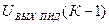на первом шаге квантования принимается равным нулю.

Выражение для определения 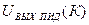принято называть рекуррентным, то есть позволяющим вычислять выходное напряжение на текущем шаге по его значению в предыдущий шаг дискретности.

.

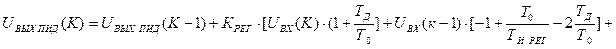
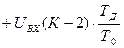Для того, чтобы исключить дифференциальную или интегральную составляющие из выходного сигнала, необходимо изменить коэффициенты в уравнении. Например, для исключения дифференциальной составляющей требуется ТД приравнять нулю. Тогда получим уравнение для ПИ-регулятора.

Для того, чтобы исключить дифференциальную или интегральную составляющие из выходного сигнала, необходимо изменить коэффициенты в уравнении. Например, для исключения дифференциальной составляющей требуется 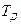приравнять нулю. Тогда получим уравнение для ПИ-регулятора.

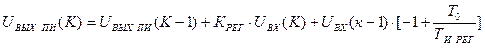. (14)

Дискретная модель ПИД -регулятора во временной области представляет собой алгебраические уравнения. Эта модель относительно легко реализуется в МПС.

Если обозначить постоянные коэффициенты в уравнении как 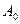, 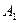и 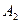, то получим более компактную запись дискретной модели регулятора:

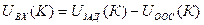. (15)

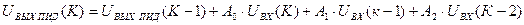. (16)

где ;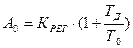

;

.

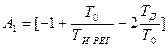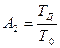Эта модель относительно легко реализуется в МПС.