Структурная схема алгоритма программной реализации цифрового ПИД - регулятора
Уравнениям (15) и (16) соответствует структурная схема модели, приведенная на рис. 3.
Представление модели в виде структурной схемы облегчает процесс программирования, т.е. создания управляющих программ для микропроцессорных систем, начинающийся с разработки алгоритма программы. На схеме наглядно видно, что требуется сделать с исходными сигналами, чтобы получить выходной сигнал. По этой модели каждую составляющую можно изменить независимо от других, и в этом ее преимущество.
В модели по формулам (15) и (16) регулирование пропорциональной, интегральной и дифференциальной частей взаимосвязано, и это является недостатком данного рекуррентного соотношения, хотя оно представляет собой наиболее простую из всех известных математических моделей регулятора.
 |
Рис. 3. Структурная схема модели цифрового ПИД-регулятора
В ранее рассмотренных моделях интегральная и дифференциальная составляющие определяются приближенно по сравнению с моделью в аналоговой форме. Более точная дискретная модель в отношении интегральной составляющей выглядит в виде следующего уравнения:
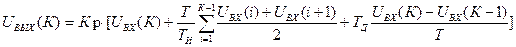 . (17)
. (17)
Если в уравнении (17) “раскрыть” сумму 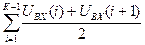 , то получим:
, то получим:
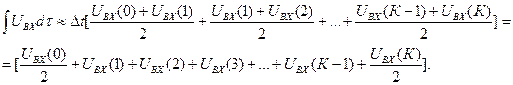 (18)
(18)
Как следует из уравнения (18) приращение интегральной составляющей при переходе с (К-1) шага квантования на К шаг для такой модели составляет
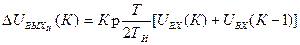 (19)
(19)
и по сравнению с ранее рассмотренной моделью требует знания входной величины (ошибки) уже для двух интервалов дискретности (  и
и 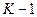 ).
).
Рекуррентное соотношение для выходного напряжения при этом варианте представления интегральной составляющей выглядит так:

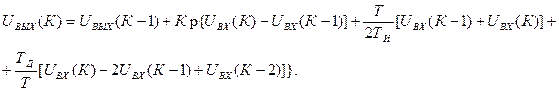 (20)
(20)
После преобразования уравнения (20)получим уравнение (21).
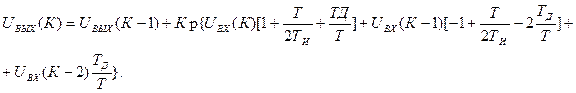 (21)
(21)
В литературе [6] приведен еще один способ получения дискретной модели ПИД-регулятора. Для этого исходное аналоговое уравнение
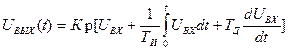 . (22)
. (22)
дифференцируют для исключения интеграла и заменяют вторую производную второй разностью. После дифференцирования получим уравнение (23).
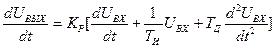 . (23)
. (23)
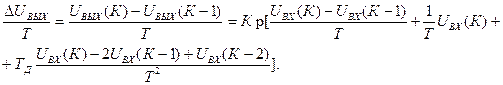 (24)
(24)
Из уравнения (24) находим выходной сигнал регулятора по формуле (25).
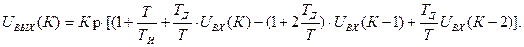 (25)
(25)
Наибольшие сложности при составлении дискретных моделей регулятора, как стало ясно из предыдущего анализа, проявляются для интегральной составляющей.
В практике управления нашли применение модели, в которых рекуррентные соотношения использовались не для всего выходного сигнала регулятора, а только для его интегральной составляющей. Это позволяет реализовать суммирование при определении интегральной части простыми средствами. Рассмотрим указанный метод и с этой целью введем следующие обозначения:
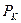 -пропорциональная часть на
-пропорциональная часть на  - шаге квантования;
- шаге квантования;
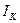 - интегральная часть на
- интегральная часть на  - шаге дискретности;
- шаге дискретности;
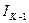 - интегральная часть на
- интегральная часть на 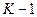 шаге квантования;
шаге квантования;
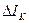 - приращение интегральной части на
- приращение интегральной части на  - шаге дискретности;
- шаге дискретности;
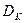 - дифференциальная часть на
- дифференциальная часть на  - шаге дискретности.
- шаге дискретности.
Тогда 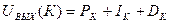 , (26)
, (26)
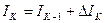 . (27)
. (27)
На первом шаге Iк-1 принимается равной нулю. Подставим выражение (27) в уравнение (26).
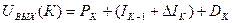 . (28)
. (28)
где 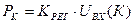 ; (29)
; (29)
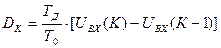 . (30)
. (30)
Интегральная составляющая на любом шаге определяется по формуле (27). На первом шаге обычно принимают
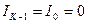 . Тогда
. Тогда 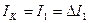 .
.
Для « 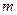 » шага
» шага 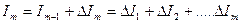 .
.
Приращение интегральной составляющей для ”дискретной модели интеграла” в виде
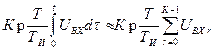 (31)
(31)
равно 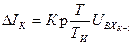 . (32)
. (32)
Для “уточненной модели интеграла”
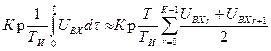
приращение 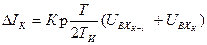 . (33)
. (33)
Структурная схема модели, соответствующая уравнениям (26 - 33), приведена на рис. 5.
Структурная схема модели, соответствующая уточненному уравнению (32) для нахождения 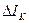 , представлена на рис. 6.
, представлена на рис. 6.
 |
Рис. 5. Структурная схема первой уточненной модели цифрового ПИД-регулятора
 |
Рис. 6. Структурная схема второй уточненной модели цифрового ПИД-регулятора
Дата добавления: 2020-10-25; просмотров: 621;











