Формальное представление игровых моделей
Для возможности анализа и поиска оптимальных решений в играх необходимо представить или задать рассматриваемую игровую модель формальным языком. В шахматах игра задается набором фигур, правилами их движения, условиями взятия фигур и постановки мата. Для описания движения фигур существует шахматная нотация, для описания стратегических и тактических действий введено множество общепринятых терминов: вилка, связка, рентген, открытая вертикаль, крепость и т.д. Однако для полного задания игры, необходимо также задать и параметры игроков: силу их игры, возможные варианты ходов, ценность ходов, функцию оценки позиций.
Далее при анализе игр будем использовать следующие обозначения:
· 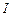 - множество игроков;
- множество игроков;
· 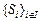 - множество стратегий игроков;
- множество стратегий игроков;
· 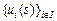 - множество функций полезности игроков;
- множество функций полезности игроков; 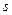 - игровая ситуация или позиция.
- игровая ситуация или позиция.
Функции полезности также иногда называют платежными функциями или функциями выигрыша. В общем случае функции полезности для игроков индивидуальны и различны. Так, функция оценка позиции (функция полезности) является одной из самых важных частей в современных шахматных компьютерах.
Функции полезности задаются для каждой возможной ситуации в игре и фактически определяют выигрыш игрока в каждой из сложившихся позиций. Некоторая ситуация 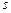 складывается, когда первый игрок выбирает некоторую стратегию
складывается, когда первый игрок выбирает некоторую стратегию 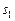 из набора возможных стратегий
из набора возможных стратегий 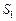 , второй игрок выбирает некоторую стратегию
, второй игрок выбирает некоторую стратегию 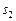 из набора возможных стратегий
из набора возможных стратегий 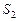 и т.д.:
и т.д.: 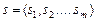 , где
, где 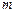 - количество игроков -
- количество игроков - 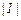 . В общем случае количество игроков может быть бесконечным.
. В общем случае количество игроков может быть бесконечным.
Множество всех возможных ситуаций в игре представляет собой декартово произведение множеств стратегий игроков:
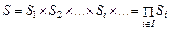 .
.
Например, в игре с тремя участниками, множество стратегий 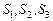 для которых непрерывны, множество ситуаций можно представить трехмерным параллелепипедом с ребрами
для которых непрерывны, множество ситуаций можно представить трехмерным параллелепипедом с ребрами 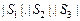 .
.
С учетом введенной терминологии, в нормальной форме игра задается как тройка множеств:
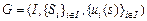 .
.
При анализе действий отдельных игроков также выделяют понятие подситуации. Подситуация 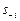 представляет собой действия (согласно выбранным стратегиям) всех игроков, за исключением игрока i. Каждую возможную ситуацию, таким образом, можно представить, как
представляет собой действия (согласно выбранным стратегиям) всех игроков, за исключением игрока i. Каждую возможную ситуацию, таким образом, можно представить, как 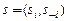 , где
, где 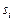 - стратегия, выбранная в рамках ситуации
- стратегия, выбранная в рамках ситуации 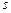 игроком i, а
игроком i, а 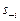 - выбор всех остальных участников игры.
- выбор всех остальных участников игры.
Биматричные игры
В экономике и управлении часто встречаются ситуации, в которых сталкиваются две или более стороны, преследующие различные цели, причем результат, полученный каждой из сторон при реализации определенной стратегии, зависит от действий других сторон.
Биматричные – статические игры двух лиц с конечными наборами стратегий.
Игры такого класса могут быть однозначно заданы двумя матрицами 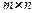 , где
, где 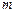 - количество стратегий игрока 1,
- количество стратегий игрока 1, 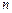 - игрока 2. Любая игровая ситуация определяется парой
- игрока 2. Любая игровая ситуация определяется парой 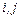 номеров стратегий, выбранных первым и вторым игроками соответственно. Выбор стратегий каждым игроком происходит независимо, без априорного знания о выборе соперника.
номеров стратегий, выбранных первым и вторым игроками соответственно. Выбор стратегий каждым игроком происходит независимо, без априорного знания о выборе соперника.
Классическим примером биматричной игры является дилемма заключенных. Задержаны два преступника, связанные некоторым общим преступлением. Прямых улик против них нет, но имеется достаточно доказательств, чтобы посадить каждого на год. Преступники содержатся и допрашиваются раздельно, причем за содействие следствию и даче показаний против соучастника, можно уйти от наказания. Если же сознаются оба, то в таком случае преступники разделят между собой наказание уже за полноценное преступление. Сроки заключений в зависимости от выбранных заключенными стратегий представлены в табл. 4.1.
Таблица 4.1
| Заключенный 1 | Заключенный 2 | |
| Молчать | Сознаться | |
| Молчать | -1, -1 | -10, 0 |
| Сознаться | 0, -10 | -5, -5 |
В таблице 4.1 выигрыши первого игрока в каждой ситуации записаны слева от запятой, а выигрыши второго игрока – справа. Множество стратегий первого игрока: {Молчать, Сознаться}. Выигрыши игроков в ситуации 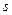 = (Сознаться; Сознаться) (выделено в таблице) равны
= (Сознаться; Сознаться) (выделено в таблице) равны 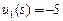 ,
, 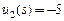 .
.
Эта задача была впервые сформулирована в 1950 г. Мерилом Фладом (Merill Flood) и Мелвином Дрешером (Melvin Dresher). Нынешнее название принадлежит Альберту Такеру (Albert Tucker). Особый интерес представляет выбор оптимальной стратегии каждым из игроков. Анализ показывает, что наиболее обоснованным решением данной игры является ситуация 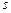 = (Сознаться; Сознаться).
= (Сознаться; Сознаться).
Дата добавления: 2020-10-25; просмотров: 596;











