Итеративный метод решения сетевых моделей

Является ли ситуация, представленная на рис. 4.5, оптимальной или устойчивой? Одним из способов анализа и решения подобных моделей является итеративный метод последовательных улучшений: последовательный выбор наилучших ответов каждым из игроков на текущую ситуацию. Алгоритм завершается устойчивой ситуацией, когда ни один из игроков не может уменьшить собственную задержку на s-t пути.

Рассмотрим более подробно следующий пример анализа сетевой игровой модели с двумя игроками (рис 4.6, а).

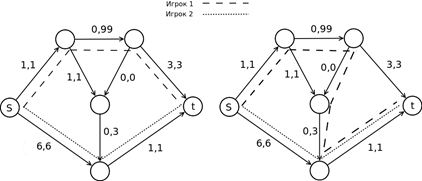
а) б)

Рис. 4.6. Итеративный метод последовательных улучшений. Начальная ситуация (а) и результат первого шага алгоритма (б)

В начальной ситуации на рис. 4.6, а задержка первого игрока составляет 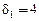, а второго 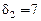. На первом шаге алгоритма первый игрок изменяет свой путь 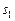и уменьшает задержку до 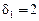, а задержка второго игрока остается без изменений: 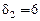. Результат представлен на рис. 4.6, б. На втором шаге алгоритма второй игрок изменяет свой путь 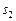(рис.4.7, а) и получает задержку 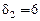, тем самым увеличивая .

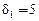Третьим шагом алгоритма первый игрок вновь изменяет путь 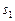и получает 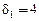, 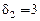(рис. 4.7, б).

Ситуация на рис. 4.7, б является равновесием по Нэшу, так как ни один из игроков не может увеличить выигрыш (уменьшить задержку) путем выбора другой стратегии (другого s-t пути) при неизменной стратегии соперника.

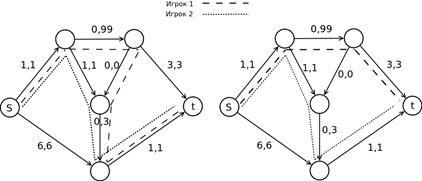
а) б)

Рис. 4.7. Итеративный метод последовательных улучшений. Результаты второго (а) и третьего (б) шагов алгоритма

На рассмотренном примере алгоритм позволил найти равновесную ситуацию за три шага, но всегда ли существует равновесие по Нэшу и достижимо ли оно в общем случае за конечное количество шагов алгоритма? Согласно теореме Розенталя, для каждой игровой сетевой модели количество шагов, улучшающих полезность участников, конечно. Отсюда следствие: в каждой сетевой игровой модели существует хотя бы одно равновесие по Нэшу (возникающее в момент, когда все шаги по улучшению полезности отдельными участниками, исчерпаны).

Доказательство теоремы строится на основе анализа специально выбранной потенциальной функции 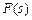, которая отображает некоторую меру загрузки всего рассматриваемого графа. 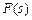монотонно уменьшается на каждом шаге алгоритма и, так как значения задержки на ребрах 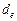являются целыми и конечными величинами, то и количество таких улучшений конечно.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Каково назначение систем и служб управления доступом к ресурсам в распределенных вычислениях?

2. Каковы основные компоненты систем пакетной обработки заданий?

3. Что такое пакет заданий?

4. Каковы основные функции систем управления ресурсами?

5. Что собой представляют специальные атрибуты конфигурирования очередей заданий?

6. Что собой представляет ресурсный запрос задания?

7. Каково назначение механизма контрольных точек?

8. Что такое архитектура OGSA (Open Grid Services Architecture)?

9. Каковы основные особенности планирования вычислений в грид на уровне приложений и потоков заданий?

10. Что такое модель задания в масштабируемой модели планирования?

11. Приведите необходимое условие разрешение конфликта параллельных задач.

12. Приведите примеры критериев эффективности распределения ресурсов.

13. Что такое модель выбора в масштабируемой модели планирования?

14. В чем заключаются основные положения метода критических работ?

15. Что такое стратегия планирования?

16. Что такое условно оптимальная стратегия планирования?

17. Что собой представляет собой параллельная схема формирования стратегии для модели задания?

18. Что собой представляет собой Парето-оптимальная стратегия планирования?

19. Что собой представляет обобщенная схема формирования стратегии для модели задания?

20. В чем состоят особенности вычислительных сред с неотчуждаемыми ресурсами?

21. Поясните понятия слота, набора и комбинации слотов для планирования пакета заданий.

22. Что такое оптимальная и эффективная комбинации слотов?

23. Что такое функция уровня ресурсных затрат?

24. Поясните назначение основных компонентов схемы циклического планирования пакета заданий.

25. Приведите формальную постановку задачи выбора оптимальной комбинации слотов.

26. Приведите функциональные уравнения схемы обратной прогонки для выбора оптимальной комбинации слотов.

27. Приведите функциональные уравнения схемы прямой прогонки выбора оптимальной комбинации слотов.

28. Поясните общую схему алгоритма отбора подходящих слотов с ранним временем старта «окна».

29. Что такое состояние системы в задаче планирования пакета независимых заданий?

30. Как оценивается эффективность той или иной комбинации слотов с помощью скалярной функции полезности?

31. Дайте определение понятию «игра». Какие существуют классификации игр?

32. Что такое равновесие по Нэшу? Насколько обоснован выбор равновесной ситуации в качестве решения игровой модели?

33. Что такое равновесие дрожащей руки? Приведите пример.

34. Какова процедура проведения аукциона второй цены? Приведите его основные свойства.

35. В чем состоят стратегии участников аукциона второй цены и как оценивается их эффективность?

36. В чем состоит парадокс Браеса? Какие Вы видите пути разрешения ситуации?

37. Каким образом осуществляется поиск решения в сетевой игровой модели? Всегда ли оно достижимо?

СПИСОК ЛИТЕРАТУРЫ

1.Конюховский, П.В., Малова, А.С. Теория игр. - М.: Юрайт, 2015. – 252 с.

2. Таненбаум, Э., ванн Стеен, М.Распределенные системы. Принципы и парадигмы. — СПб.: Питер, 2003. – 877 с.

3. Таненбаум, Э.Архитектура компьютера.— СПб.: Питер, 2002. – 704 с.

4. Топорков, В.В. Модели распределенных вычислений. – М.: ФИЗМАТЛИТ, 2004. – 320 с.