Аналитическое представление проективных преобразований

Любое проективное преобразование однозначно определяется парой реперов R(Е₁ , Е₂ , Е₃ , Е) и R′(Е′₁ , Е′₂ , Е′₃ , Е′). Так как реперы заданы, тогда можно найти преобразование координат при переходе от одного репера к другому, т.е. можно найти матрицу А причем она не вырождена (почему?).

Формулы преобразования координат одной и той же точки Х будут:

λ Х_R =A∙X_R′ и μ X_R′ = А^-1 ∙ Х_R (*)

Пусть f (Х) = Х ', причем Х_R 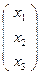и Х '_R′ .

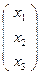Найдем координаты точки Х ' в репере R:λ Х '_R =A∙Х '_R′ .

Таким образом, λ Х '_R =A∙Х_R , тогда μ Х = A^-1 ∙f (Х) (**)

(Почему существует обратная матрица?)

Замечание: Хотя формулы (*) и (**) вроде бы одинаковые, необходимо помнить, что в (*) одна и та же точка в разных реперах, в (**) две разные точки (образ и прообраз) в одном репере.

Матрица, задающая преобразование координат для двух данных реперов R(Е₁ , Е₂ , Е₃ , Е) и R′(Е′₁ , Е′₂ , Е′₃ , Е′) единственна (с точностью до пропорциональности). Отсюда следует, что проективное преобразование задает единственную матрицу A (с точностью до пропорциональности).

Теорема. Если на Р₂ задано отображение формулами (**), тогда это отображение является проективным преобразованием.

Доказательство. Пусть f : Р₂ → Р₂ , так что λ f (Х)=A∙Х.

Рассмотрим точки репера Е₁ , Е₂ , Е₃ , Е , их образы обозначим

Е′₁ , Е′₂ , Е′₃ , Е′. Необходимо и достаточно доказать что точки

Е′₁ , Е′₂ , Е′₃ , Е′ образуют новый репер (т.е никакие три не лежат на одной прямой и он согласован).

Пусть матрица A = 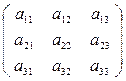,тогда Е′₁= f (Е₁)= A· = ,

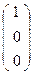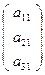Е′₂= f (Е₂)= A· 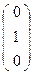= 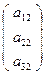, Е′₃=f(Е₃)=A· 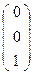= 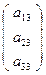, Е′=f(Е)=A· =

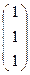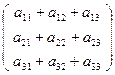
Е′₁ , Е′₂ , Е′₃ - не лежат на одной прямой, так как 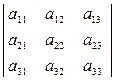≠0 (почему?),

То же самое можно сказать о тройках: Е′₁ , Е′₂ , Е′, Е′₁ , Е′₃ , Е′, Е′₂ , Е′₃ , Е′.

Т.к., Е′₁ + Е′₂+ Е′₃= Е′ - есть согласованность (проверьте).

Таким образом, f : R(Е₁ , Е₂ , Е₃ , Е) → R′(Е′₁ , Е′₂ , Е′₃ , Е′), а значит f - есть проективное преобразование. □

Вывод: Проективное преобразование однозначно определяется формулами (**), то есть матрицей A. Поэтому это тоже можно считать определением проективного преобразования.

Определение: Композицией двух проективных преобразований f : Х → Х′ и g : Х′ → Х′′ будем называть последовательное выполнение преобразований сначала f затем g.

Обозначение: f ◦ g

При этом f : R→ R′ и g : R′ → R′′ , значит f ◦ g : R → R′′, т.о., f◦g - проективное преобразование.

(почему?).

Пусть f задается матрицей A, а g задается матрицей В.

Тогда f◦g(Х)=f(g(Х))=f(A·Х)=В(A·Х)=В·A·Х,

таким образом матрицей преобразования f◦g является матрица В·A, причем она не вырождена. (почему?).

Определение: Преобразование, оставляющее все точки плоскости на месте, называется тождественным.

Тождественное преобразование задается матрицей – Е.

Определение: Обратным преобразованием для f : Х → Х′ будет преобразование f ^-1: Х′ → Х .

Если f : R → R′ ,

тогда f ^-1 : R′ → R.

f ^-1 - проективное преобразование (почему?).

f ^-1 будет задаваться - А^-1 (почему?).

Теорема. Множество П - проективных преобразований является группой относительно операции композиция.

Доказательство. Самостоятельно.

Теорема. Проективное преобразование прямой образует подгруппу в группе проективных преобразований - П.

Доказательство. Самостоятельно.

Виды проективных преобразований:

1. Инволюция – нетождественное проективное преобразование , совпадающее со своим обратным: f = f ^-1.

2. Коллинеация - проективное преобразование, при котором прямая переходит в прямую, точка переходит в точку.

3. Корреляция - проективное преобразование, при котором прямая переходит в точку, точка переходит в прямую.

4. Гомология - проективное преобразование, имеющее по крайней мере три неподвижных точки принадлежащие одной прямой.

5. Центральное проектирование.

Множество коллинеаций образует подгруппу в группе проективных преобразований. Подгруппа коллинеаций сама имеет несколько подгрупп. Эта идея («групповая») была положена в основу классификации геометрических преобразований Феликсом Клейном в 1872 году в работе «Сравнительное обозрение новейших геометрических исследований». Другое название этой работы - «Эрлангенская программа».

Геометрия – это учение о геометрических преобразованиях и каждая геометрия характеризуется соответствующей группой преобразований. Предметом геометрии являются те свойства фигур, которые инвариантны при преобразованиях данной группы.

Евклидова геометрия изучает те свойства фигур, которые сохраняются при движениях - Д (длины, углы). Аффинная геометрия изучает те свойства фигур, которые сохраняются при аффинных преобразованиях - А (простое отношение точек, параллельность прямых). Проективная геометрия изучает те свойства фигур, которые сохраняются при проективных преобразованиях - П (сложное отношение точек, инцидентность, точка, прямая, пучок, репер, квадрики).

Д А П

Перспектива

Определение: Центральной проекцией или перспективой прямой ℓ на прямую ℓ' из точки S называется отображение при котором каждой точке А прямой ℓ ставится в соответствие точка А'прямой ℓ' такая что А'= ℓ' ∩ (SА).

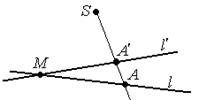
Свойства:

1. Перспектива является взаимнооднозначным отображением в силу того, что любые две прямые имеют одну и только одну общую точку.

2. При перспективе сохраняется сложное отношение четырёх точек лежащих на одной прямой (по свойствам сложного отношения).

3. Если обозначить ℓ ∩ ℓ' = М , тогда точка М отображается сама в себя, т.е. при перспективе прямой на прямую точка пересечения этих прямых переходит сама в себя.

Доказательство. Пусть М → М′ ≠ М,

по определению М ′=(SМ)∩ℓ ', но М ℓ′ 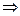М = ℓ'∩(SМ). □

Теорема1. Для того, чтобы отображение прямой на прямую было перспективой необходимо и достаточно чтобы при этом отображении точка пересечения этих прямых переходила в себя.

Доказательство. Необходимость следует из свойства (3).

Достаточность: 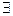φ: ℓ₁ → ℓ₂ и 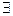М : φ(М)=М, причем М= ℓ₁∩ℓ₂ .

Возьмем точки А₁ , В₁ 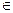ℓ₁ , найдем φ(А₁)=А₂ и φ(В₁)=В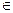₂ ℓ₂ .

Таким образом φ : А₁ , В₁ , М → А₂ , В₂ , М , причем это отображение единственное, но (А₁В₁)∩(А₂В₂)=S - единственная точка. Отсюда следует, что существует перспектива прямой ℓ₁ на прямую ℓ₂ из точки S .

Так как отображение единственное - это и есть перспектива. □

Теорема 2. Пусть даны две тройки точек: А₁, В₁, С₁ 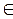ℓ₁ и А₂, В₂, С₂ 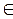ℓ₂ , причем в каждой тройке точки различны, тогда 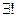φ : ℓ₁ → ℓ₂ , такое что φ(А₁)=А₂ , φ(В₁)=В₂ , φ(С₁)=С₂.

Доказательство. Докажем построением. Возможны два случая.

1 случай: ℓ₁ ≠ ℓ₂ .

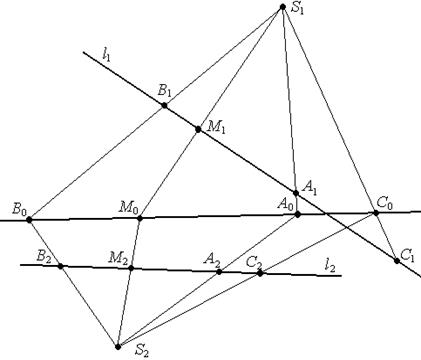
1. Проводим прямую (А₁А₂) и берем на ней две произвольные точки S₁ и S₂ отличные от А₁ и А₂ .

2. В₀ =(S₁В₁)∩(S₂В₂), С₀ =(S₁С₁)∩(S₂С₂), А₀ =(В₀С₀)∩(S₁S₂),

3. Рассмотрим отображения φ₁ : ℓ₁ → (В₀С₀) - перспектива с центром S₁ и φ₂ : (В₀С₀) → ℓ₂ - перспектива с центром S₂, тогда искомое проективное преобразование φ = φ₂ ◦ φ₁ . так как φ₁ и φ₂ - проективные преобразования, то φ - тоже проективное преобразование.

4. М₀ =(S₁М₁)∩(В₀С₀), М₂ =(S₂М₀)∩ ℓ₂ - образ точки М₁.

2 случай ℓ₁ = ℓ₂ .

1. Проводим произвольную прямую ℓ₃ , берем произвольную т. S₃ не инцидентную прямым ℓ₁ и ℓ₃ .

2. А₃=(S₃А₁)∩ ℓ₃ ,

В₃=(S₃В₁)∩ ℓ₃ ,

С₃=(S₃С₁)∩ ℓ₃ .

3. Проводим прямую (А₂А₃) и берем на ней две произвольные точки S₁ и S₂ отличные от А₂ и А₃ .

4. С₀ =(S₁С₃)∩(S₂С₂), В₀ =(S₁В₃)∩(S₂В₂), А₀ =(В₀С₀)∩(S₁S₂).

5. Рассмотрим отображения:

φ₃ : ℓ₁ → ℓ₃ - перспектива с центром S₃

φ₁ : ℓ₃ → (В₀С₀) - перспектива с центром S₁

φ₂ : (В₀С₀) → ℓ₁ = ℓ₂ - перспектива с центром S₂,

тогда искомое проективное преобразование

φ = φ₂ ◦ φ₁ ◦ φ₃ .

6. М₃=(S₃М₁)∩ℓ₃, М₀ =(S₁М₃)∩(В₀С₀), М₂ =(S₂М₀)∩ℓ₁ .

Вывод: Проективное отображение прямой на прямую задается двумя тройками различных точек.

Вывод:Любое проективное отображение прямой можно разложить на композицию не более трех перспектив:

1. Если ℓ₁ = ℓ₂ - три перспективы.

2. Если ℓ₁ ≠ ℓ₂ - не более двух перспектив.

3. Если ℓ₁ ≠ ℓ₂ и (А₁А₂)∩(В₁В₂)∩(С₁С₂)= S - одна перспектива с центром в точке S.