Архивация, обработка и представление результатов
Для сбора данных была создана архивная матрица, включавшая разделы от паспортных данных до результатов гемодинамического мониторинга и показателей послеоперационного течения. После заполнения матрицы данные перекодировались в формат среды интерпретации "MatLab", в которой нами были написаны программы (файлы-сценарии) их обработки. Исключение составляла база данных по кардиохирургическим пациентам ДГБ № 1, созданная в формате "Microsoft Access-98".
Учитывая отсутствие априорной информации о виде распределений величин изучаемых переменных в наших выборках, мы считали возможным использовать для их обработки только непараметрические статистические критерии. С другой стороны, поскольку выбор точек разделения градаций любого признака всегда математически произволен и приводит к потере некоторого не равного нулю количества информации, для целей исследования оказалось возможным использование только тех критериев, которые не предполагают градуировки величин.
Совместное выполнение двух названных условий сводило выбор критерия для сравнения пары переменных разного типа практически к одному варианту — критерию инверсий Уилкоксона. Для пары булевских переменных был избран точный метод Фишера, для пары вещественных использовался традиционный коэффициент линейной корреляции Пирсона Rxy. Обработка результатов исследования осуществлялась с помощью пакета "MatLab" (версии 31 и 5.2) на ПК серий Pentium и Pentium-II.
Помимо традиционной табличной и графической форм представления результатов, в настоящем исследовании использована специальная форма графического представления данных на основе системы прямоугольных координат "АСИ — ДИОПСС", изображенная на рис. 7.
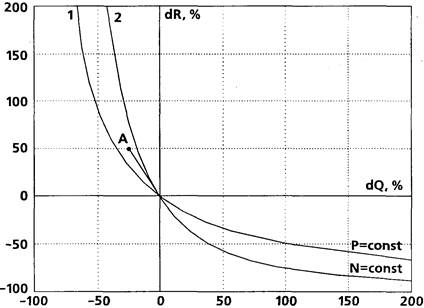
Рисунок 7.
По оси абсцисс отложена линейная шкала изменений СИ, выраженных в процентах по отношению к исходному значению, соответствующему началу координат (точка 0). Шкала ординат, отражающая динамику ИОПСС, построена аналогично. В такой системе координат переходные процессы, при которых остаются неизменными уровни среднего АД и расхода мощности левым желудочком, могут быть представлены функциями достаточно простого вида.
Гипербола 1 представляет собой линию равного среднего АД — геометрическое место точек соответствующих исходной величине САД в выбранном диапазоне шкал. Таким образом, изменения САД при перестройке режима кровообращения не происходит в том и только в том случае, если точка, отражающая новый набор параметров, лежит на кривой 1. Сектор плоскости, лежащий правее и выше кривой 1, соответствует более высоким величинам САД по сравнению с исходным (в точке 0), а левее и ниже нее — более низким. Аналогично кривая 2 представляет собой линию равной мощности левого желудочка; маневр параметрами кровообращения, осуществленный по закону N = const, предполагает, что точка, отражающая новое состояние гемодинамики, лежит на гиперболе 2. Сектор плоскости, расположенный выше и правее этой кривой, отражает режимы гемодинамики с более высоким расходом мощности ЛЖ по отношению к исходному (в точке 0), а сектор левее и ниже кривой — с более низким. Уравнения кривых 1 и 2 в данной системе координат записались, соответственно, как
ΔИОПСС1 = 70000. (ΔСИ+ 100)-1 - 100, (14)
ΔИОПСС2= 10000 • (ΔСИ+100) -2 -100. (15)
В качестве примера на графике изображен переход режима кровообращения из точки, соответствующей началу координат, в точку А, характеризующуюся снижением СИ на 25% и возрастанием ИОПСС на 50% по отношению к исходным значениям этих параметров. Видно, что переход 0—>А сопровождается повышением САД, на снижением расхода мощности левого желудочка по отношению к их исходным значениям.
Описанный график позволяет анализировать динамические процессы относительно четырех важнейших показателей кровообращения в большом круге и, с нашей точки зрения, увеличивает степень наглядности за счет привлечения представлений векторного анализа.
Дата добавления: 2020-11-18; просмотров: 722;











