Сетевые игровые модели и парадокс Браеса

Сетевые модели и игры трафика (congestion games), как раздел теории игр, впервые были определены в 1973 году Робертом Розенталем (Robert W. Rosenthal). В качестве примеров применения теории игр в сетевых моделях можно привести моделирование транспортных сетей или прохождение интернет траффика. В планировании распределенных вычислений с помощью сетевых моделей можно моделировать выполнение сложноструктуированных заданий с зависимостями по данным, а также возникновение задержек при передаче данных между узлами и доменами вычислительных узлов. В подобных моделях значение имеет не только кратчайший путь от вершины отправления до вершины назначения, важным фактором является уровень загрузки ресурсов: объем трафика в различных ветвях сети и связанные с ним задержки.

Сетевая модель задается ориентированным графом, ветви которого представляют собой магистрали и каналы передачи данных, а вершины - пункты пересадки, перекрестки или точки разделов сети, маршрутизаторы и т.п.

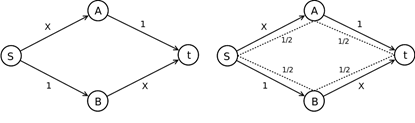
В качестве примера сетевой задачи можно привести парадокс Браеса. Рассмотрим модель на рис. 4.3, а: каждый день большое количество автомобилей совершает поездку из пригородного города S в промышленный и бизнес центр – город t. Причем существует два различных S-t маршрута: транзитом через город A или через город B.

Качество и продолжительность магистралей между городами различно. Так, дороги S-B и A-t имеют много полос, покрывают большое расстояние, и вне зависимости от уровня траффика время перемещения по ним составляет 1 час (соответствующее время отмечено на ребре на рис. 4.3, а). Дороги S-A и B-t относительно короткие, но однополосные, поэтому время движения x по ним пропорционально загруженности движения. Например, если дорогу S-A-t выберут 2/3 от общего количества участников движения S-t, то время в пути до города A для каждого в среднем составит 2/3 часа или 40 минут.

Возникает вопрос, возможно ли в такой системе равновесие и каким образом оно достигается. Очевидно, что каждый участник движения стремиться минимизировать время в пути и каждый следующий день будет выбирать тот путь, который по его предыдущему опыту обеспечивает наименьшую задержку. Логично предположить, что из-за симметричности путей S-A-t и S-B-t после некоторого периода переходных процессов потоки движения распределятся между ними равномерно.

На рис. 4.3, б пунктирной линией представлены два потока с уровнем загрузки 0.5. Время в S-t пути, таким образом, составляет 0.5+1 = 1.5 часа на каждом из маршрутов.

а б

Рис. 4.3. Парадокс Браеса. Первоначальная структура сети (а) и распределение траффика (б)

Данная ситуация, очевидно, является равновесной, так как ни одному из участников невыгодно изменять собственный маршрут: с добавлением нового участника загруженность нового маршрута незначительно, но превысит 0.5, а значит время в пути будет больше по сравнению со старым маршрутом.

а б

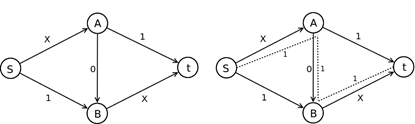
Рис. 4.4. Парадокс Браеса. Модифицированная структура сети (а) и новое распределение траффика (б)

Предположим далее, что администрация области решила радикально улучшить транспортную систему и в экспериментальном режиме установила между городами A и B телепортер, позволяющий мгновенно перемещаться по маршруту A-B. Модифицированная структура сети представлена на рис. 4.4, а и включает в себя ребро A-B с весом 0.

С учетом этой модификации новое равновесное распределение траффика представлено на рис. 4.4, б пунктирной линией: весь поток движется по единственному маршруту S-A-B-t, уровень его загрузки равен 1, а среднее время в пути: x + 0 + x = 2 часа. Действительно, при попытке какого-либо из участников изменить маршрут и срезать через дороги S-B или A-t, его время в пути останется неизменным: 1+x = 2 часа. Путь A-A-B-t при этом станет немного быстрее из-за отклонения одного участника и, тем самым, более выгодным по сравнению с объездным путем.

Таким образом, данное кажущееся улучшение транспортной сети с применением новых технологий на треть увеличивает среднее время в пути для всех участников движения. При этом пути S-A-t и S-B-t остались неизменными и при равномерном распределении траффика между ними (как на рис. 4.3, б), без использования телепортера A-B, можно уменьшить время в пути обратно до 1.5 часов. Однако с учетом рационального эгоистичного поведения каждого участника такое равномерное распределение траффика не является устойчивым в модифицированной структуре сети: каждому участнику выгодно воспользоваться телепортером, пока им не воспользовались другие, и уменьшить время в пути до 1 часа.

Стоит отметить, что данный парадокс не является чисто умозрительным, и подобные закономерности наблюдаются, например, в компьютерных сетях и в физических процессах.