Многоагентное взаимодействие и равновесные ситуации
Равновесие по Нэшу
Пример биматричной игры в табл. 4.1 демонстрирует, что даже в игре размером 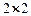 может быть неочевидно, какую стратегию поведения стоит выбирать каждому из игроков. Один из подходов к решению подобных моделей – выделение равновесных ситуаций, к которым должны сходиться рациональные игроки.
может быть неочевидно, какую стратегию поведения стоит выбирать каждому из игроков. Один из подходов к решению подобных моделей – выделение равновесных ситуаций, к которым должны сходиться рациональные игроки.
Понятие равновесия (по Нэшу) в некоалиционных играх было предложено Джоном Нэшем (John Forbes Nash) в диссертации и серии работ 1950-1953 гг.
Ситуация 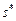 в игре
в игре 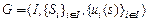 называется равновесием по Нэшу, если для любого игрока
называется равновесием по Нэшу, если для любого игрока 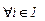 выполняется:
выполняется:
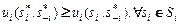 . (4.2.1)
. (4.2.1)
Таким образом, равновесие по Нэшу, это такая ситуация в игре, от которой ни одному из игроков невыгодно отклоняться в одиночку.
Рассмотрим также отображения, которые для каждого игрока в каждой возможной подситуации 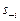 ставят в соответствие некоторую стратегию
ставят в соответствие некоторую стратегию 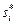 - наилучший ответ:
- наилучший ответ:
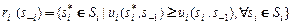 .
.
При этом 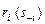 называют отображением отклика игрока. Из (4.2.1) следует, что равновесие по Нэшу - это ситуация, образуемая наилучшими ответами каждого игрока на наилучшие ответы остальных игроков:
называют отображением отклика игрока. Из (4.2.1) следует, что равновесие по Нэшу - это ситуация, образуемая наилучшими ответами каждого игрока на наилучшие ответы остальных игроков: 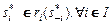
К примеру, игра дилемма заключенных (см. табл. 4.1) имеет единственное равновесие по Нэшу: (Сознаться; Сознаться). Действительно, ни одному из заключенных невыгодно отклоняться от данной ситуации поодиночке. Если один заключенный решит сменить стратегию с Сознаться на Молчать, то этим он только уменьшит свой выигрыш с 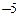 до
до 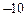 . Одновременно, положение второго игрока улучшится (выигрыш увеличится с
. Одновременно, положение второго игрока улучшится (выигрыш увеличится с 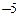 до
до 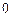 ), и тому тоже невыгодно будет менять стратегию.
), и тому тоже невыгодно будет менять стратегию.
Стоит отметить, что равновесная ситуация в данной игре не является эффективным решением. Ситуация (Молчать; Молчать) максимизирует сумму выигрышей для игроков. Однако недостаток данной ситуации в неустойчивости: каждому игроку выгодно сменить стратегию на признание и предать соперника (подельника). В этом смысле дилемма заключенных демонстрирует разницу между равновесием по Нэшу и оптимальностью по Парето.
Равновесие по Нэшу - необязательно выгодная, но устойчивая ситуация. С другой стороны, ситуация оптимальна по Парето в том случае, когда полезность ни одного из участников не может быть увеличена без уменьшения полезностей других участников.
Упрощенная игровая модель взаимодействия граждан в обществе аналогична дилемме заключенных и представлена в виде биматричной игры в табл. 4.2.
Таблица 4.2
| Гражданин 1 | Гражданин 2 | |
| Альтруизм | Эгоизм | |
| Альтруизм | 2, 2 | -1, 2+ε |
| Эгоизм | 2+ ε, -1 | 0, 0 |
Множества стратегий поведения игроков одинаковы 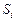 ={Альтруизм; Эгоизм},
={Альтруизм; Эгоизм}, 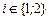 .При ε > 0 у каждого игрока всегда есть мотивация отклониться от ситуации общего блага (Альтруизм; Альтруизм), и рациональный игрок должен им воспользоваться. Таким образом, равновесием по Нэшу является устойчивая ситуация (Эгоизм; Эгоизм).
.При ε > 0 у каждого игрока всегда есть мотивация отклониться от ситуации общего блага (Альтруизм; Альтруизм), и рациональный игрок должен им воспользоваться. Таким образом, равновесием по Нэшу является устойчивая ситуация (Эгоизм; Эгоизм).
Из приведенных определений и примеров можно сделать вывод, что рациональным игрокам (соперникам), стремящимся максимизировать собственный выигрыш, а также гарантировать некоторое минимальное значение выигрыша, следует разыгрывать равновесные ситуации.
Подобными биматричными моделями можно представить множество различных проблем принятия решений, например, понижение/повышение цен на предлагаемые товары (ресурсы) конкурирующими фирмами, конфликт ядерных держав и т.п.
Дата добавления: 2020-10-25; просмотров: 615;











