Параметрические кубические кривые.

Параметрическая кубическая кривая задаётся тремя уравнениями.

x(t)=a_xt³+b_xt²+c_xt+d_x

y(t)=a_yt³+b_yt²+c_yt+d_y

z(t)=a_zt³+b_zt²+c_zt+d_z

Параметр t лежит в пределах от 0 до 1. Нам необходимо знать все коэффициенты уравнений, чтобы однозначно определить положение кривой в пространстве. В определении коэффициентов всегда используют производные.

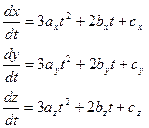
Производные определяют касательный вектор к данной кривой. Записывают уравнения параметрических кубических кривых в различном виде. Наиболее известны форма Эрмита и форма Безье. В последнее время, в связи с развитием пространственного проектирования сложных объектов используют форму записи в виде B-сплайнов.

1) Рассмотрим форму Эрмита.

Исходными данными являются точки: касательная P₁, конечная P₄ и касательная вектора в этих точках. Это один приближающий участок.

R₁

P₄ R₄

P₁

Для кривой более сложной формы на следующем участке конечная точка становится начальной и добавляется новая конечная.

R₄’

R₁

P₄ R₄ P₄’

P₁

Таких участков может быть сколь угодно много.

X(0) = P_1x

X’(0) = R_1x

Аналогично по всем координатам. В конечной точке P₄:

X(1) = P_4x

X’(1) = R_4x

…

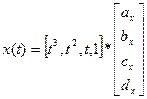это равно С_х

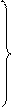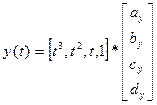
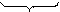T

Аналогично z(t).

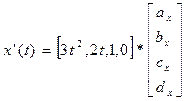
Совершенно аналогично для производных.

y’(t) и z’(t) аналогично.

Подставим в x(t) и x’(t) 0 и 1:

x(0) = P_1x = [0, 0, 0, 1]* C_x

x(1) = P_4x = [1, 1, 1, 1]* C_x

x’(0) = P_1x = [0, 0, 1, 0]* C_x = R_4x

x’(1) = P_4x = [3, 2, 1, 0]* C_x = R_4x

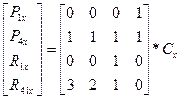
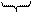
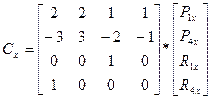
Эрмитова

матрица G_hx

x(t)=TM_hG_hx

y(t)=TM_hG_hy

z(t)=TM_hG_hz

Свойства.

1. Если перемешаем точки, то не получится использовать ту же запись, то есть сложно организовать интерактивный режим, нет относительных координат.

2. Вектора R₄ и R₄‘ не стыкуются, следовательно куски стыкуются не гладко.

2) РассмотриРаР

м форму Безье. Запись выглядит чуть лучше.

При записи в форме Безье исходными являются координаты четырёх точек.

P₂

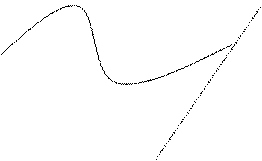P₁ P₄

P₃

P₁, P₂, совпадают с вектором касательной в точке P₁; P₃, P₄ – с вектором касательной в точке P₄. И к ним опущены перпендикуляры.

Исходные данные – координаты точек P₁, P₂, P₃, P₄. Математически вывели, что касательный вектор определяется по формуле:

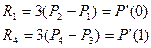
Вектор Эрмита:

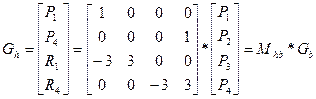
матрица вектор

Безье Безье

Тогда x(t)=T*M_hb*M_h*G_b=T*M_b*G_b, где

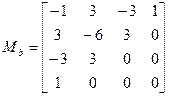
Таким образом, матрицы M_h(цифровая)_b, M_b – числовые. В G_b подставляем координаты четырёх точек и получаем пространственное представление кривой третьего порядка.

1. Эта форма записи пригодна для использования в интерактивных режимах.

2. В точках сопряжения двух отрезков производная непрерывна и поверхность получается сглаженной без изломов.

3. Многоугольник, который образуют четыре точки всегда выпуклый. Это свойство позволяет резко упростить функции отсечения.

2) В-сплайн. Сам по себе термин сплайн перешёл в графику из кораблестроение. Там сплайн – это гибкая металлическая линейка, которая используется при нанесении разметки на корпус корабля. В-сплайн никогда не проходит по всем точкам, которые необходимы для его постройки. Выполняет сразу же функцию сглаживания.

Пример.

Запись уравнения В-сплайна отличается матрицей в формуле стоящей на втором месте и заданием векторов.

x(t) = T*M_s*G_sx, где

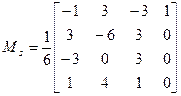
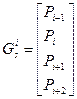, где 2 £ i £ n-2

Берём первые 4 точки, рисуем участок, затем сдвиг на одну и т.д. Эти кусочки стыкуются друг с другом. Линия эта непрерывна, выполняется функция частичного сглаживания далеко стоящих точек. В настоящее время широко применяется в описании сложных 3D объектов. Особенно выгодно, когда есть макет изделия, если его склеить, получим погрешности, применим В-сплайн, получим обтекаемую поверхность. Применяется в самолётостроении.