Полигональная сетка.

Представляет собой совокупность плоских многоугольников. Многоугольники связаны между собой. Количество вершин у многоугольников не ограничено. Способ задания является неточным. Погрешности существенны для тел сложной формы, хотя теоретически любой сложности тело можно представить отрезками плоскостей.

Например, шестигранник ещё не похож на цилиндр, а 12-гранник его уже больше напоминает. Чем больше плоскостей, тем точнее мы подгоним фигуру. Следует помнить, что чем точнее приближение, тем дольше происходит математическая обработка описания и тем больше требуется использовать памяти.

Параметрические кубические прямые описывают поверхность через уравнения третьего порядка.

f(x, y, z), причём уравнений записывается три. f – это многочлен третьего порядка.

x = f₁(y, z, t)

y = f₂(x, z, t)

z = f₃(x, y, t)

Существует целый набор способов представления. Число участков сразу же снижается, сложность вычислений возрастает. Всё равно сложное тело описать одним уравнением не получится. Как описывать полигоны?

Например, здесь 2 куска поверхности с разными описаниями, а вообще их может быть и больше.

Способы описания полигональной сетки:

1) Явное задание многоугольников.

2) С помощью указателей в списке вершин.

3) Список рёбер.

1. P – многоугольник. P=((x₁, y₁, z₁), (x₂, y₂, z₂), (x₃, y₃, z₃), … , (x_n, y_n, z_n)). Причём точки в перечислении записываются строго в порядке обхода многоугольника. Последняя n-я точка соединяется с первой в записи. Фигура – это совокупность многоугольников.

F = {P₁, P_{2, … ,}P_n}

Пример. F = {P₁, P_2, P₂}

P₁=((x₁, y₁, z₁), (x₂, y₂, z₂), (x₇, y₇, z₇))

P₂=((x₇, y₇, z₇), (x₆, y₆, z₆), (x₈, y₈, z₈), (x₉, y₉, z₉))

P₃=((x₃, y₃, z₃), (x₄, y₄, z₄), (x₅, y₅, z₅), (x₆, y₆, z₆), (x₇, y₇, z₇))

2 3 4

I III

1 9 7

II

5

8 6

– мы прорисовывали 2 раза. Это не модно. Координаты точки 7 входят несколько раз. Мы дублируем одни и те же данные. Точка, участвующая в описании двух сторон будет записываться дважды, трёх сторон – трижды и так далее. Объём хранимой информации явно завышен. Существуют математические способы определения общих участков пространственных кривых, но количество сравнений для выполнения таких отсечений становится неоправданно большим. Также редактировать такие ссылки очень сложно. Способ этот громоздкий, но легко доступный для понимания.

2. 1) Составляется предварительный список вершин, не обязательно по возрастанию номеров:

(x₁, y₁, z₁),

(x₂, y₂, z₂)

…

(x₉, y₉, z₉)

В этом списке ни одна точка не повторяется дважды. Затем ориентируясь на номер записи в списке вершин описывают полигон.

P₁=(1, 2, 7)

P₂=(6, 7, 9, 8)

P₃=(3, 4, 5, 6, 7)

Сами записи проще, занимают меньший объём памяти, гораздо проще редактировать фигуру.

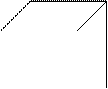
z

7 6

2 3

8 5 x

1 4

y

1 – (010)

2 – (011)

3 – (111)

4 – (110)

5 – (100)

6 – (101)

7 – (001)

8 – (000)

Полный куб:

P₁=(1, 8, 5, 4)

P₂=(1, 2, 3, 4)

P₃=(2, 7, 6, 3)

P₄=(7, 6, 5, 8)

P₅=(1, 2, 7, 8)

P₆=(3, 6, 5, 4)

Повторение перерисовывания общих рёбер не убрано.

3. Явное задание рёбер. При явном задании рёбер также первоначально составляется список вершин.

а) V₁

V₂

…

V₉

б) На основании этого списка составляется список рёбер.

E₁= {1; 2}

E₂= {2; 7}

E₃= {7 ;1}

…

В этой записи для избежания пересечений, указывается, какому полигону принадлежит ребро и фиктивный параметр рисовать или не рисовать (a и ù a).

E₁= {1; 2; P₁; a}

E₂= {2; 7; P₁; a}

E₃= {7 ;1; P₁; P₂; a}

Если мы ХЗ ХЗ ХЗ ХЗ.

E₄= {7; 6; P₂; a}

E₅= {6; 8; P₂; a}

E₆= {8 ;9; P₂; a}

E₇= {9 ;7; P₂; ù a}

E₁ E₂

E₃

1

3 E₇ 7

E₆ E₄

8 6

E₅

Из списка рёбер записывается полигон.

P₁=( E₁, E₂, E₃)

P₂=( E₇, E₄, E_5, E₆)

Исходя из совокупностей рёбер исключив пересечения, составляется описание полигональной сетки. На первый взгляд такое описание сложнее. В самом деле, объём описания не намного больше, но обрабатывается с такой же скоростью.