Основы теории проверки статистических гипотез. Параметрические критерии.
1. В прикладных задачах часто требуется по наблюдениям выборки высказать некоторое суждение (гипотезу) относительно интересующих экспериментатора характеристик генеральной совокупности, из которой эта выборка извлечена. То есть, речь идет о проверке статистических гипотез.
Гипотеза – это некоторое предположение о параметрах известных распределений (параметрическая) или о виде неизвестного закона распределения (непараметрическая) случайных величин, выдвигаемое в качестве предварительного, условного объяснения.
Теория проверки статистических гипотез является основным инструментом доказательной, а не интуитивной медицины.
Задачи медицинских и биологических исследований, для решения которых необходимо сформулировать статистические гипотезы:
· анализ соответствия распределения значений признака в изучаемой группе какому-либо определенному закону (анализ соответствия распределения нормальному закону);
· сравнение групп по параметрам распределений признака (по средним значениям, дисперсиям).
Например, при проверке статистических гипотез можно получить ответ на следующий вопрос. В двух однородных группах больных гриппом была проведена вакцинация: одной лекрственным средством «А», а другой - «В», среднее время выздоровления в группах неодинаково. Указывает ли это обстоятельство на то, что одно противогриппозное средство по эффективности превосходит другое или же выявленное различие случайно?
Для решения любой подобной задачи выдвигаются две статистические гипотезы:
· нулевая гипотеза Н0 - гипотеза об отсутствии различий между группами, либо об определенных значениях параметров, либо о соответствии распределения нормальному закону;
· альтернативная гипотеза Н1 - гипотеза о существовании различий между группами, либо об отличающихся от заданных значениях параметров, либо о несоответствии распределения нормальному закону.
Нулевая гипотеза формулируется таким образом, чтобы она была противоположной той исследовательской (медицинской, биологической) гипотезе, которая послужила поводом для проведения исследования.
Для проверки нулевой гипотезы применяют статистические методы (тесты, критерии).
Статистика – это функция от выборочных наблюдений, на основе которой принимается или отвергается нулевая гипотеза.
Статистическими критериями называются правила, согласно которым выясняется, соответствует или нет интересующая нас гипотеза опытным данным.
Статистические критерии - это наиболее широко применяемые статистические средства.
Значение критерия, которое рассчитано по выборочной совокупности, подчиняющейся определённому закону распределения, называется наблюдаемым.
Множество возможных значений статистического критерия, при которых основная гипотеза принимается, называется областью принятия.
Множество возможных значений статистического критерия, при которых основная гипотеза отвергается, называется критической областью.
Точки, разграничивающие критическую область и область принятия гипотезы, называются критическими точками.
При проверке статистических гипотез возникают следующие виды ошибок:
· ошибка первого рода – это вероятность отвергнуть правильную нулевую гипотезу;
· ошибка второго рода – это вероятность принять неправильную нулевую гипотезу.
2. Уровень значимости - это максимально приемлемая для исследователя вероятность ошибочно отклонить нулевую гипотезу, когда на самом деле она верна, т.е. допускаемая исследователем величина ошибки первого рода.
При иссследованиях в фармации, медицине и биологии используется величина уровня значимости, равная 0,05. При разработке стандартов используют уровень значимости равный 0,01.
Уровень значимости или вероятность ошибки первого рода обозначается через «р», а вероятность ошибки второго рода - через «γ».
Доверительная вероятность (γ) - это вероятность не совершить ошибку первого рода и принять верную гипотезу Н0 (γ=1-р).
Важнейшей характеристикой любого статистического критерия является его мощность. Мощностью критерия называется его способность правильно исключать ложную гипотезу.
Мощность оценивается вероятностью 1-γ, где γ - вероятность ошибки второго рода.
3. Схема проверки статистических гипотез:
1) Выдвигаются две гипотезы: основная (нулевая) «Н0» и альтернативная (конкурирующая) «Н1».
2) Задается уровень значимости «р». Статистический вывод никогда не может быть сделан со стопроцентной уверенностью. Всегда допускается риск принятия неправильного решения. При проверке статистических гипотез мерой такого риска является уровень значимости «р».
3) По исходным данным, т.е. по выборке, вычисляется наблюдаемое (эмпирическое, расчетное) значение критерия.
4) По специальным статистическим таблицам определяется табличное (критическое) значение критерия.
5) Путем сравнения наблюдаемых и табличных значений делается вывод о правильности той или иной гипотезы.
4. В процессе медико-биологических исследований часто возникает проблема сравнения результатов обследования (например, в контрольной и экспериментальной группах или до и после эксперимента).
Для решения этой проблемы существует большое количество статистических критериев. Каждый из них имеет свою специфику, отличаясь друг от друга (например, типами данных, объемами выборок, количеством сравниваемых выборок, качеством сравниваемых выборок (зависимая и независимая) и др.).
Наиболее популярным из таких критериев является t-критерий Стьюдента, который применяется примерно в 30-40% научных медицинских работ (рисунок 2.1).

Рисунок 2.1. Соотношение статистических методов, используемых в медицинских научных работах
t-критерий Стьюдента - метод проверки однородности выборок, позволяет принять или отвергнуть гипотезу о равенстве средних двух выборок ( 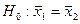 ).
).
Данный критерий был разработан английским химиком Уильямом Госсеттом (1876-1936 гг.) (рисунок 2.2) для оценки качества пива в компании «Гиннес».
Статья Госсета вышла в 1908 г. в журнале «Биометрика» под псевдонимом «Student» (Студент).

Рисунок 2.2. У. Госсет
t-критерий Стьюдента используется:
· при проверке гипотезы о равенстве средних двух независимых выборок (двухвыборочный t-критерий). Вэтом случае анализируются контрольная и экспериментальная выборки разных объемов. Например, группа больных сахарным диабетом и группа здоровых людей;
· при проверке гипотезы о равенстве средних двух зависимых выборок (парный t-критерий). В этом случае анализируется одна и та же выборка, но до и после эксперимента.Например, средняя частота пульса у одних и тех же пациентов до и после приема антиаритмического препарата.
Применение критерия Стьюдента возможно, если выполняются следующие два условия:
· рассматриваемые выборки имеют нормальное распределение;
· дисперсии рассматриваемых выборок равны.
Исследователями установлено, что оба условия одновременно выполняются лишь в 4-5% случаев медико-биологических экспериментов.
В то же время анализ диссертаций, научных работ, статей, опубликованных в медицинских журналах, показывает, что t-критерий Стьюдента используется при проведении статистических расчетов в 50% работ.
5. Схема применения двухвыборочного критерия Стьюдента:
1) Н0: 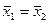 .
.
Н1: 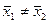 .
.
1) р=0,05 - уровень значимости.
2) 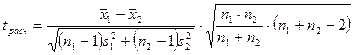 , (2.1)
, (2.1)
где n1, n2 - объемы рассматриваемых выборок, 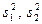 - дисперсии рассматриваемых выборок,
- дисперсии рассматриваемых выборок, 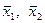 - сравниваемые средние значения выборок.
- сравниваемые средние значения выборок.
4) 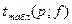 ,
,
где f= n1+n2-2- число степеней свободы (табличное значение).
5) Если 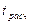 ≤
≤ 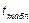 , то «H0» принимается.
, то «H0» принимается.
Если 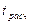 >
> 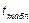 , то «H0» отвергается.
, то «H0» отвергается.
Критерий Стьюдента применяется в случае малых выборок (n1,2≤30).
Пример 2.1. Если при родах шейка матки долго не раскрывается, то продолжительность родов увеличивается и может возникнуть необходимость кесарева сечения. Ученые решили выяснить, ускоряет ли гель с простагландином Е2 раскрытие шейки матки. В исследование вошло 2 группы рожениц. Роженицам первой группы вводили в шейку матки гель с простагландином Е2, роженицам второй группы вводили гель-плацебо. В обеих группах было по 21 роженице возраст, рост и сроки беременности были примерно одинаковы. Роды в группе, получавшей гель с простагландином Е2, длились в среднем 8,5 часов (стандартное отклонение 4,7 часа), в контрольной группе - 13,9 часа (стандартное отклонение 4,1 часа). Можно ли утверждать, что гель с простагландином Е2 сокращал продолжительность родов?
Решение.
1) Н0: 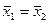 .
.
Н1: 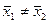 .
.
2) р=0,05 - уровень значимости.
3) Используем формулу (2.1).
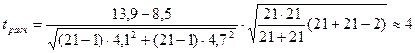 .
.
4) 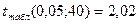 .
.
5) Т.к. 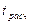 >
> 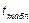 , то «H0» отвергается, т.е. гель с простагландином Е2 сокращал продолжительность родов.
, то «H0» отвергается, т.е. гель с простагландином Е2 сокращал продолжительность родов.
6. Схема применения парного критерия Стьюдента:
1) Н0: 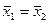 .
.
Н1: 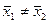 .
.
2) р=0,05- уровень значимости.
3) 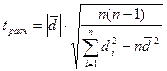 , (2.2)
, (2.2)
где 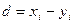 - разности между соответствующими значениями пар переменных,
- разности между соответствующими значениями пар переменных, 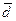 - среднее значение этих разностей, n - объем выборки.
- среднее значение этих разностей, n - объем выборки.
4) 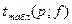 ,
,
где f= n-1- число степеней свободы (табличное значение).
5) Если 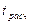 ≤
≤ 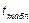 , то «H0» принимается.
, то «H0» принимается.
Если 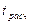 >
> 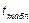 , то «H0» отвергается.
, то «H0» отвергается.
Иногда сравнение выборочных средних проводится по следующей формуле:
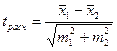 , (2.3)
, (2.3)
где 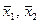 - сравниваемые средние величины; m1 и m2 - ошибки сравниваемых средних величин.
- сравниваемые средние величины; m1 и m2 - ошибки сравниваемых средних величин.
Если tрасч³2, то «H0» отвергается.
Пример 2.2. Для оценки эффективности нового гипогликемического препарата были проведены измерения уровня глюкозы в крови пациентов, страдающих сахарным диабетом, до и после приема препарата:
| № пациента | Уровень глюкозы в крови, моль/л | |
| до приема препарата | после приема препарата | |
| 9,6 | 5,7 | |
| 8,1 | 4,2 | |
| 8,8 | 6,4 | |
| 7,9 | 5,5 | |
| 9,2 | 5,3 | |
| 8,0 | 5,2 | |
| 8,4 | 5,1 | |
| 10,1 | 5,9 | |
| 7,8 | 7,5 | |
| 8,1 | 5,0 | |
| Среднее значение | 8,6 | 5,6 |
Решение.
1) Н0: 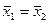 .
.
Н1: 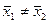 .
.
2) р=0,05- уровень значимости.
3)
| № пациента | Уровень глюкозы в крови, моль/л | Разность значений 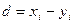
|
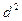
| |
| до приема препарата | после приема препарата | |||
| 9,6 | 5,7 | 3,9 | 15,21 | |
| 8,1 | 4,2 | 3,9 | 15,21 | |
| 8,8 | 6,4 | 2,4 | 5,76 | |
| 7,9 | 5,5 | 2,4 | 5,76 | |
| 9,2 | 5,3 | 3,9 | 15,21 | |
| 8,0 | 5,2 | 2,8 | 7,84 | |
| 8,4 | 5,1 | 3,3 | 10,89 | |
| 10,1 | 5,9 | 4,2 | 17,64 | |
| 7,8 | 7,5 | 0,3 | 0,09 | |
| 8,1 | 5,0 | 3,1 | 9,61 | |
| Сумма | 30,2 | 103,22 |
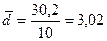 .
.
Используем формулу (2.2).
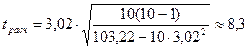 .
.
4) 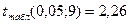 .
.
5) Т.к. 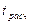 >
> 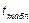 , то «H0» отвергается, т.е. уровень глюкозы в крови после приема препарата снизился, значит новое средство эффективно.
, то «H0» отвергается, т.е. уровень глюкозы в крови после приема препарата снизился, значит новое средство эффективно.
Пример 2.3. У студентов - медиков проводилось исследование пульса до и после сдачи экзамена. Частота пульса до экзамена составила 98,8 ±4,0, а после экзамена 84,0 ±5,0. Можно ли считать, что после экзамена частота пульса снижается и приближается к норме?
Решение.
1) Н0: 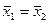 .
.
Н1: 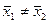 .
.
2) р=0,05.
3) Используем формулу (2.3).
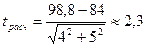 .
.
4) Т.к. tрасч>2, то «H0» отвергается, т.е. после экзамена частота пульса снижается и приближается к норме.
5. Литература:
1. Васильева Л.А. Статистические методы в биологии, медицине и сельском хозяйстве: Учеб. пособие для вузов. - Новосибирск, Новосибирский Государственный университет, 2007. - 128 с
2. Герасимов А.Н. Медицинская статистика: Учеб. Пособие. – М.: МИА, 2007. - 480 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов.- 9-е изд., стер. - М.: Высш. шк., 2003. - 479 с.
4. Кендалл М., Стюарт А. Статистические выводы и связи. - М.: Наука, 1973. - 470 с.
5. Лобоцкая Н.Л. Высшая математика. / Н.Л. Лобоцкая, Ю.В. Морозов, А.А. Дунаев. - Мн.: Высшая школа, 1987. - 319 с.
6. Медик В.А., Токмачев М.С., Фишман Б.Б. Статистика в медицине и биологии: Руководство. В 2-х томах/ Под ред. Ю.М. Комарова. Т. 1. Теоретическая статистика. - М.: Медицина, 2000. - 412 с.
7. Основы высшей математики и математической статистики: Учебник / И.В. Павлушкин и соавт. - М.: ГЭОТАР-МЕД, 2004. - 424 с.
8. Петри А., Сэбин К. Наглядная медицинская статистика / А. Петри, К. Сэбин; пер. с англ. под ред. В.П. Леонова. 2-е изд., перераб. и доп. - М.: ГЭОТАР-Медиа, 2009. - 168 с.
9. http://matstats.ru/
Дата добавления: 2016-10-07; просмотров: 5101;











