Круговые и переходные кривые.
Для плавного закругления трассы при ее поворотах в углы вписывают круговые кривые- дуги окружностей.
Круговая кривая характеризуется углом поворота и радиусом R. Угол поворота измеряется в точке В — вершине угла поворота. (Рис. 14.3.)
Основные элементы круговой кривой:
Т - тангенс;
К - длина кривой;
Б - биссектриса;
Д – домер;
R – радиус;
φ – угол поворота.
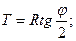
| 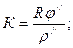
| (14.2) |
| Д = 2Т- К ; | 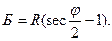
|
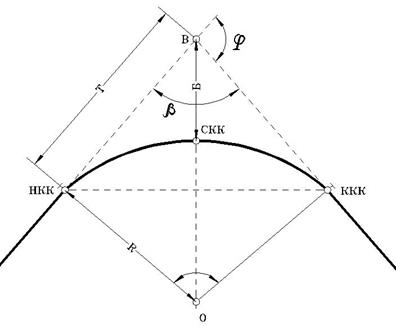
Рис. 14.3.
Главными точками круговой кривой являются:
Ø начало круговой кривой - НКК;
Ø середина круговой кривой - СКК;
Ø конец круговой кривой - ККК.
При большой скорости движения для более плавного входа поездов на кривую и сход с кривой вписывают переходные кривые.
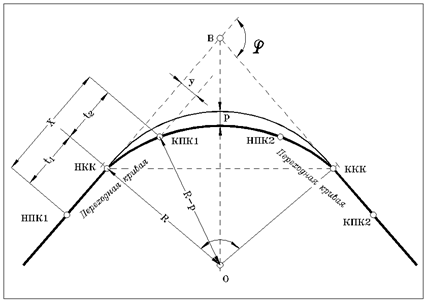
Рис. 14.4.
Например на железных дорогах переходные кривые предусматриваются для всех закруглений, радиус которых менее 2 000 метров. В настоящее время в качестве переходной кривой используется радиальная спираль /клатоида/ уравнение которой имеет вид:
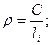
| (14.3) |

где ρ— переменный радиус круговой кривой,
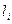 — текущая длина переходной кривой от ее начала до точки i,
— текущая длина переходной кривой от ее начала до точки i,
С — параметр переходной кривой.
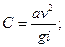
| (14.4) |
где а — ширина колеи железнодорожного пути,
v — расчетная скорость движения поезда,
i — уклон возвышения наружного рельса,
g — ускорение свободного падения.
В зависимости от величины R длину переходной кривой определяют по формуле
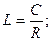
| (14.5) |
В результате устройства переходных кривых круговая кривая смещается к центру на величину р
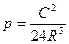 или или 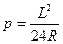 ; ;
| (14.6) |
Радиус смещенной кривой будет равен R – р.
Элементы переходной кривой определяются по формулам:
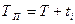 ; ; 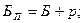
| |
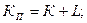
| (14.7) |
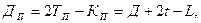
|
где 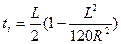 .
.
Угол поворота переходной кривой в радианной мере равен
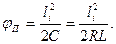
| (14.8) |
Дата добавления: 2017-05-02; просмотров: 5108;











